题目内容
19.假设我国发射的一颗探月卫星绕月球做匀速圆周运动,卫星的轨道半径为r,运动周期为T,月球半径为R,引力常量为G,根据上述已知条件可得到( )| A. | 卫星的加速度为$\frac{{4π}^{2}}{T^2}$(R+r) | |
| B. | 卫星绕月球做匀速圆周运动的线速度为$\frac{2πR}{T}$ | |
| C. | 月球的质量为$\frac{{{4π}^{2}{r}^{3}}}{{GT}^{2}}$ | |
| D. | 月球表面的重力加速度为$\frac{{{4π}^{2}{r}^{3}}}{{{T}^{2}{R}^{2}}}$ |
分析 卫星绕月球做匀速圆周运动,根据万有引力提供向心力,以及万有引力等于重力求解.
解答 解:A、卫星绕月球做匀速圆周运动,卫星的轨道半径为r,运动周期为T,根据圆周运动公式得卫星的加速度为a=$\frac{{4π}^{2}}{T^2}$r,故A错误;
B、根据圆周运动公式得卫星绕月球做匀速圆周运动的线速度为v=$\frac{2πr}{T}$,故B错误;
C、卫星绕月球做匀速圆周运动,根据万有引力提供向心力,有:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{T^2}$r,
M=$\frac{{{4π}^{2}{r}^{3}}}{{GT}^{2}}$,故C正确;
D、根据万有引力等于重力得:
$\frac{GMm}{{R}^{2}}$=mg
月球表面的重力加速度为g=$\frac{{{4π}^{2}r}^{3}}{{{T}^{2}R}^{2}}$,故D正确;
故选:CD.
点评 解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论,并能熟练运用.

练习册系列答案
相关题目
10.有关宇宙的理解,下列说法中正确的是( )
| A. | 质量越大的恒星寿命越长 | |
| B. | 太阳发出的光和热来自于碳、氧等物质的燃烧 | |
| C. | 在天空中呈现暗红色的恒星的温度比呈现白色的恒星的温度高 | |
| D. | 由于光速有限,因此观察遥远的天体就相当于观察宇宙的过去 |
7.在物理学中,原子,原子核及其更深层次的粒子统称为微观粒子,以下关于微观粒子的相关论述正确的是( )
| A. | 由大到小的关系为:分子→原子→原子核→质子→夸克 | |
| B. | 纳米科学技术的研究对象是比原子更小的微粒 | |
| C. | 物质的不同物态表现出不同的性质是由分子的排列决定的,与分子力无关 | |
| D. | 原子核几乎占据了原子的全部空间,电子绕着原子核高速旋转 |
14. 一简谐横波沿x轴正向传播,在t=0时刻的波形如图所示,此时该波刚传到x=8m处,再经过3.8s时,P质点第5次出现波峰.下列说法正确的是( )
一简谐横波沿x轴正向传播,在t=0时刻的波形如图所示,此时该波刚传到x=8m处,再经过3.8s时,P质点第5次出现波峰.下列说法正确的是( )
 一简谐横波沿x轴正向传播,在t=0时刻的波形如图所示,此时该波刚传到x=8m处,再经过3.8s时,P质点第5次出现波峰.下列说法正确的是( )
一简谐横波沿x轴正向传播,在t=0时刻的波形如图所示,此时该波刚传到x=8m处,再经过3.8s时,P质点第5次出现波峰.下列说法正确的是( )| A. | t=0时P点振动方向沿y轴正方向 | |
| B. | 该波的波速为5m/s | |
| C. | 再经过△t=1.6s,x=2m处的质点向前传播△x=8m | |
| D. | 再经过△t=1.4s,坐标为x=16m处的质点第一次出现波峰 |
11.2014年10月24日,嫦娥五号飞行试验成功发射,首次试验从月球返回的技术.嫦娥五号飞行试验器由轨道器、返回器、上升器和着陆器组成,到达环月轨道后,着陆器和上升器落到月面上轨道器和返回器将继续围绕月球做匀速圆周运动以等待上升器从月面返回后进行交会对接.下列关于嫦娥五号飞行试验器的说法中正确的是(引力常量G已知)( )
| A. | 由于轨道器与返回器在围绕月球做匀速圆周运动的过程中处于完全失重状态,所以其不受月球的引力作用 | |
| B. | 若已知轨道器与返回器围绕月球做匀速圆周运动的周期T和距月球表面的高度h,就可以计算出月球的平均密度ρ | |
| C. | 若已知月球的平均密度ρ和月球的半径R,就可以计算出月球表面的重力加速度g | |
| D. | 先让上升器与轨道器和返回器在同一个圆形轨道上,然后让上升器加速,即可实现与轨道器和返回器的对接 |
3. 目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )
目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )
 目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )
目前智能手机普遍采用了电容触摸屏.电容触摸屏是利用人体的电流感应进行工作的,它是一块四层复合玻璃屏,玻璃屏的内表面和夹层各涂一层ITO(纳米铟锡金属氧化物),夹层ITO涂层作工作面,四个角引出四个电极,当用户触摸电容触摸屏时,用户手指和工作面形成一个电容器,因为工作面上接有高频信号,电流通过这个电容器分别从屏的四个角上的电极中流出,且理论上流经四个电极的电流与手指头到四角的距离成比例,控制器通过对四个电流比例的精密计算来确定位置.对于电容触摸屏,下列说法正确的是( )| A. | 电容触摸屏只需要触摸,不需要压力即能产生位置信号 | |
| B. | 使用绝缘笔,在电容屏上也能进行触控操作 | |
| C. | 手指压力变大时,由于手指与屏的夹层工作面距离变小,电容变小 | |
| D. | 手指与屏的接触面积变大时,电容变小 |
4.如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为固定电阻.开关S是闭合的,V1、V2和V3为理想电压表,读数分别为U1、U2和U3;A1、A2和A3为理想电流表,读数分别为I1、I2和I3.U1数值不变,现断开S,下列推断中正确的是( )
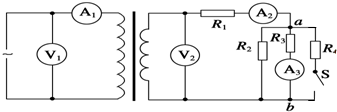

| A. | U2变小、I3变小 | B. | U2不变、I3变小 | C. | I1变小、I2变小 | D. | I1变小、I2变大 |
