题目内容
如图所示，在倾角为θ的斜面上放置一内壁光滑的凹槽A，凹槽A与斜面间的动摩擦因数μ＝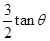
，槽内紧靠右挡板处有一小物块B，它与凹槽左挡板的距离为d．A、B的质量均为m，斜面足够长．现同时由静止释放A、B，此后B与A挡板每次发生碰撞均交换速度，碰撞时间都极短．已知重力加速度为g．求：
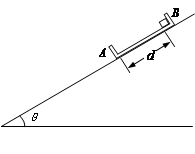
（1）物块B从开始释放到与凹槽A发生第一次碰撞所经过的时间t1．
（2）B与A发生第一次碰撞后，A下滑时的加速度大小aA和发生第二次碰撞前瞬间物块B的速度大小v2．
（3）凹槽A沿斜面下滑的总位移大小x．
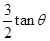，槽内紧靠右挡板处有一小物块B，它与凹槽左挡板的距离为d．A、B的质量均为m，斜面足够长．现同时由静止释放A、B，此后B与A挡板每次发生碰撞均交换速度，碰撞时间都极短．已知重力加速度为g．求：（1）物块B从开始释放到与凹槽A发生第一次碰撞所经过的时间t1．
（2）B与A发生第一次碰撞后，A下滑时的加速度大小aA和发生第二次碰撞前瞬间物块B的速度大小v2．
（3）凹槽A沿斜面下滑的总位移大小x．
（1）
（2）
（3）x=d
（2）（3）x=d 试题分析：（1）设B下滑的加速度为aB，则
A所受重力沿斜面的分力
所以B下滑时，A保持静止
解得
（2）释放后，B做匀加速运动，设物块B运动到凹槽A的左挡板时的速度为v1，根据匀变速直线运动规律得
第一次发生碰撞后瞬间A、B的速度分别为v1、0，此后A减速下滑，则
解得
，方向沿斜面向上 A速度减为零的时间为t1，下滑的位移大小为x1，则
在时间t1内物块B下滑的距离
，所以发生第二次碰撞前凹槽A已停止运动，则B下滑距离x1与A发生第二次碰撞 
解得
（3）方法一：设凹槽A下滑的总位移为x，由功能关系有
解得 x=d
方法二：由（2）中的分析可知
第二次碰后凹槽A滑行的距离
同理可得，每次凹槽A碰后滑行的距离均为上一次的一半，则
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
