Question

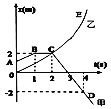
【题目】滑板运动是一项刺激运动项目，深受青少年喜欢，某次比赛部分赛道如图甲所示，现将赛道简化为如图乙所示的模型：粗糙倾斜轨道AB与光滑圆弧形轨道相切于B点，粗糙水平轨道CD与光滑圆弧形轨道BC、DE相切于C、D点。运动员与滑板一起（可看作质点）从A点静止开始滑下，经轨道BC、CD滑到E点时速度恰好为零，然后返回。己知人和滑板总质量为m=60kg，倾斜轨道AB长L=5m，与水平面的夹角θ=53°，滑板与AB的动摩擦因数为μ1=0.2，水平轨道CD长S=6m，圆弧形轨道半径均为R=4m，不计空气阻力，（sin53°=0.8，cos53°=0.6，g取10m/s2）。求：

(1)运动员第一次滑到C点时对轨道的压力大小；

(2)滑板与水平轨道CD的动摩擦因数；

(3)运动员从A点开始下滑到第一次回到AB轨道速度为零的过程损失的机械能。

Answer 1

【答案】(1)2100N；(2)；(3)1670J。

【解析】

(1)运动员从A到C的过程由动能定理得：

mgLsin53°+mgR（1-cos53°）-μ1mgcos53°L=mvc2

代入数据解得

vc=10m/s

在C点有

解得

FN=2100N

有牛顿第三定律可知，运动员第一次滑到C点时对轨道的压力大小为2100N
(2)由(1)问可得：vc=10m/s，运动员从C到E的过程由动能定理得

-μ2mgS-mgR=0-mvC2

解得

μ2=

(3)运动员从E点到回到AB最高点过程由动能定理

mgRcos53°-μ2mgS-mgxsin53°-μ1mgxcos53°=0

解得

损失的机械能