题目内容
11.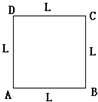 一质点从如图所示的边长为L的正方形轨道的一个顶点开始沿轨道做匀速率运动,质点运动速率为v,在运动过程中:
一质点从如图所示的边长为L的正方形轨道的一个顶点开始沿轨道做匀速率运动,质点运动速率为v,在运动过程中:(1)质点沿轨道运动n周后回到A点时,其通过的路程为4nL,位移为0.
(2)在运动过程中质点通过最大位移大小为$\sqrt{2}L$,方向为从A指向C,并在图中标出最大位移.
(3)若以从A点开始运动为计时起点t=0,则每次通过最大位移所对时刻为(n-1)$\frac{4L}{v}$+$\frac{2L}{v}$(n=1,2,3…).
分析 路程等于物体运动轨迹的长度,位移的大小等于首末位置的距离
解答 解:(1)路程等于运动轨迹的长度,s=n•4L=4nL.位移x=0.
(2)当物体运动到对角线上的对顶点时,位移大小最大,x=$\sqrt{{L}^{2}+{L}^{2}}=\sqrt{2}L$,方向为从A指向C,如图: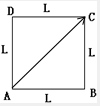
(3)第一次经过最大位移的时间为t1=$\frac{2L}{v}$,再运动一周第二次经过最大位移处,周期T=$\frac{4L}{v}$,
则每次通过最大位移所对时刻为t=(n-1)$\frac{4L}{v}$+$\frac{2L}{v}$(n=1,2,3…)
故答案为:(1)4nL;0;(2)$\sqrt{2}L$;从A指向C;如图;(3)(n-1)$\frac{4L}{v}$+$\frac{2L}{v}$(n=1,2,3…)
点评 解决本题的关键知道位移和路程的区别,知道位移的大小等于首末位置的距离,路程等于运动轨迹的长度.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
19.物体同时受到在一个平面内的三个共点力的作用,下列几组力中合力不可能使物体处于平衡状态的是( )
| A. | 5N,7N,8N | B. | 5N,2N,3N | C. | 1N,5N,10N | D. | 10N,10N,10N |
16.下列不属于液体表面张力作用具有收缩趋势而引起的现象是( )
| A. | 小昆虫停留在水面上 | |
| B. | 用焊锡焊接处总是球形的 | |
| C. | 液体流不过网眼很密的筛子 | |
| D. | 具有收缩趋势的雨水掉到游禽羽毛上时,雨水不能湿润羽毛 |

 如图所示,质量m=2.0×10-2kg的带电小球用绝缘细线竖直地悬挂于电场中,当小球的带电量为q1=+1.0×10-4C时,悬线中的张力为T1=1.5×10-1N,g=10m/s2求:
如图所示,质量m=2.0×10-2kg的带电小球用绝缘细线竖直地悬挂于电场中,当小球的带电量为q1=+1.0×10-4C时,悬线中的张力为T1=1.5×10-1N,g=10m/s2求: