题目内容
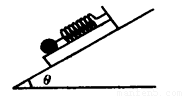
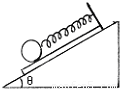
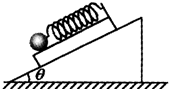为了测量小木板和斜面间的摩擦因数，某同学设计如图所示实验，在小木板上固定一个轻弹簧，弹簧下端吊一个光滑小球，弹簧长度方向与斜面平行，现将木板连同弹簧、小球放在斜面上，用手固定木板时，弹簧示数为F1，放手后，木板沿斜面下滑，稳定后弹簧示数为F2，测得斜面斜角为θ，则木板与斜面间动摩擦因数为多少？（斜面体固定在地面上）
解：设小球的质量为m，木扳与小球的总质量为M，木板与斜面间的动摩擦因数为?，由题意得：
F1=mgsinθ… ①
放手后，木板和小球沿斜面向下匀加速运动，由牛顿第二定律得：
Mgsinθ-?Mgcosθ=Ma…②
对小球有：mgsinθ-F2=ma…③
由式①、式②、式③得：
μ=
tan θ
答：木板与斜面间动摩擦因数为tan θ．
分析：木板固定时，弹簧秤的示数为F1，根据平衡条件求出重力沿斜面向下的分力．当放手后木板沿斜面匀加速下滑时，根据牛顿第二定律分别对整体和小球列方程，得到加速度的表达式，再联立求解动摩擦因数．
点评：本题是测量动摩擦因数的一种方法，实质是整体法和隔离法的综合应用，基础题．
F1=mgsinθ… ①
放手后，木板和小球沿斜面向下匀加速运动，由牛顿第二定律得：
Mgsinθ-?Mgcosθ=Ma…②
对小球有：mgsinθ-F2=ma…③
由式①、式②、式③得：
μ=
tan θ答：木板与斜面间动摩擦因数为
tan θ．分析：木板固定时，弹簧秤的示数为F1，根据平衡条件求出重力沿斜面向下的分力．当放手后木板沿斜面匀加速下滑时，根据牛顿第二定律分别对整体和小球列方程，得到加速度的表达式，再联立求解动摩擦因数．
点评：本题是测量动摩擦因数的一种方法，实质是整体法和隔离法的综合应用，基础题．
练习册系列答案
小学课时特训系列答案
相关题目
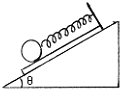为了测量小木板和斜面间的动摩擦因数，某同学设计了如下的实验．在小木板上固定一个弹簧秤（弹簧秤的质量可不计），弹簧秤下吊一个光滑小球．将木板连同小球一起放在斜面上．如图所示，木板固定时，弹簧秤的示数为F1，放手后木板沿斜面下滑，稳定时弹簧秤的示数是F2，测得斜面的倾角为θ．由测量的数据可以计算出小木板跟斜面间动摩擦因数为
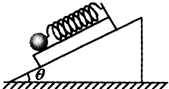为了测量小木板和斜面间的摩擦因数，某同学设计如图所示实验，在小木板上固定一个轻弹簧，弹簧下端吊一个光滑小球，弹簧长度方向与斜面平行，现将木板连同弹簧、小球放在斜面上，用手固定木板时，弹簧示数为F1，放手后，木板沿斜面下滑，稳定后弹簧示数为F2，测得斜面斜角为θ，则木板与斜面间动摩擦因数为多少？（斜面体固定在地面上）
定一个轻弹簧，弹簧下端吊一个光滑小球，弹簧长度方向与斜面平行，现将木板连同弹簧、小球放在斜面上，用手固定木板时，弹簧示数为F
，放手后，木板沿斜面下滑，稳定后弹簧示数为F
，测得斜面斜角为θ，则木板与斜面间动摩擦因数为多少？（斜面体固定在地面上）
