题目内容
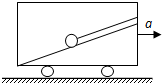 水平直轨道上运动的火车车厢内有一个倾角为37°的光滑斜面,斜面上有一个质量为m=0.5kg的小球,用轻绳系于斜面的顶端,如图所示.若火车以加速度a=15m/s2向右加速运动,求绳子的拉力大小和斜面对小球支持力的大小.(g=
水平直轨道上运动的火车车厢内有一个倾角为37°的光滑斜面,斜面上有一个质量为m=0.5kg的小球,用轻绳系于斜面的顶端,如图所示.若火车以加速度a=15m/s2向右加速运动,求绳子的拉力大小和斜面对小球支持力的大小.(g=10m/s2,sin37°=0.6,cos37°=0.8).
分析:首先判断小球是否飞离了斜面,根据小球刚刚飞离斜面的临界条件,即绳子的倾角不变,斜面的支持力刚好为零,解出此时的加速度与题目给出的加速度大小进行比较,若给出加速度大于小球的临界加速度说明小球已经飞离了斜面,否则小球还在斜面上.
解答:解:当加速度a较小时,小球与斜面一起运动,此时小球受重力、绳子拉力和斜面的支持力,绳子平行于斜面;当加速度a足够大时,小球将飞离斜面,此时小球仅受重力与绳子的拉力作用,绳子与水平方向的夹角未知,而题目要求出当斜面以15m/s2的加速度向右做加速运动时,绳的拉力及斜面对小球的弹力,必须先求出小球离开斜面的临界加速度a0,(此时小球所受斜面的支持力恰好为零)小球的受力如图:
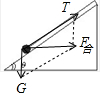
由牛顿第二定律得:
F合=mgcotθ=ma0
解得:
a0=gcotθ=10×
=13.3m/s2
因为:
a=15m/s2>a0
所以小球一定离开斜面N=0,小球的受力如图所示:
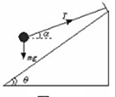
则水平方向有牛顿第二定律得:
Tcosα=ma
竖直方向有受力平衡得:
Tsinα=mg
由以上两式整理得:
T=
=
≈9.01N
N=0
答:绳的拉力为9.01N,斜面对小球的弹力为零.

由牛顿第二定律得:
F合=mgcotθ=ma0
解得:
a0=gcotθ=10×
| 4 |
| 3 |
因为:
a=15m/s2>a0
所以小球一定离开斜面N=0,小球的受力如图所示:

则水平方向有牛顿第二定律得:
Tcosα=ma
竖直方向有受力平衡得:
Tsinα=mg
由以上两式整理得:
T=
| (ma)2+(mg)2 |
| (0.5×15)2+(0.5×10)2 |
N=0
答:绳的拉力为9.01N,斜面对小球的弹力为零.
点评:此题最难解决的问题是小球是否飞离了斜面,我们可以用假设法判断出临界加速度来进行比较.

练习册系列答案
相关题目
 在水平直轨道上运动的火车厢内有一个倾角θ=30°的光滑斜面,如图所示,小球的重力为mg,绳对球的拉力为FT、斜面对小球的弹力为FN,当火车以加速度a向左运动时( )
在水平直轨道上运动的火车厢内有一个倾角θ=30°的光滑斜面,如图所示,小球的重力为mg,绳对球的拉力为FT、斜面对小球的弹力为FN,当火车以加速度a向左运动时( ) 在水平直轨道上运动的火车厢内有一个倾角θ=30°的光滑斜面,如图所示,小球的重力为mg,绳对球的拉力为FT、斜面对小球的弹力为FN,当火车以加速度a向左运动时
在水平直轨道上运动的火车厢内有一个倾角θ=30°的光滑斜面,如图所示,小球的重力为mg,绳对球的拉力为FT、斜面对小球的弹力为FN,当火车以加速度a向左运动时
