题目内容
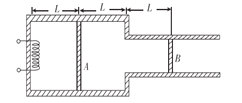
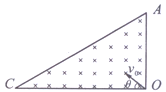
【题目】如图所示,折射率为n=![]() 的正方形透明板ABCD的四周是空气,AB边长为3
的正方形透明板ABCD的四周是空气,AB边长为3![]() a,点光源S1位于透明板的中分线MN上,S1与AB边相距a,它朝着AB边对称射出两条光线,入射角为i=60°,只考虑一次反射,求两条光线入射到AB后的交点到CD的距离?
a,点光源S1位于透明板的中分线MN上,S1与AB边相距a,它朝着AB边对称射出两条光线,入射角为i=60°,只考虑一次反射,求两条光线入射到AB后的交点到CD的距离?
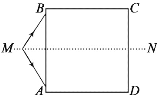
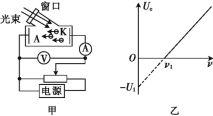
【答案】(3![]() -2
-2![]() )a
)a
【解析】
两入射光关于MN对称,则折射光必相交于MN上,根据对称性做出光路图,如图所示:
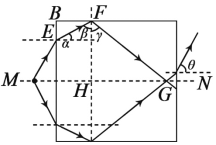
光从透明板射向空气时的临界角为
C=arcsin![]() =45°
=45°
根据折射定律可知
n=![]()
解得:
![]()
则
sinβ=![]() >
>![]() =sinC,
=sinC,
则在BC面上发生全反射,根据反射定律可知γ=β
应用数学知识可知
lBF=(1.5![]() a-
a-![]() a)tanβ=
a)tanβ=![]() a
a
lGH=(1.5![]() a)tanγ=
a)tanγ=![]() a
a
则G到CD的距离
L=3![]() a-lBF-lGH=(3
a-lBF-lGH=(3![]() -2
-2![]() )a
)a

练习册系列答案
相关题目