题目内容
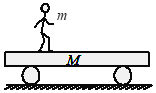
【题目】如图所示,静止在光滑水平面上的长木板![]() ,质量
,质量![]() ,长
,长![]() ,与
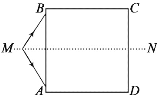
,与![]() 等高的固定平台
等高的固定平台![]() 长
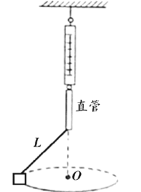
长![]() ,平台右侧有一竖直放置且半径
,平台右侧有一竖直放置且半径![]() 的光滑半圆轨道
的光滑半圆轨道![]() .质量
.质量![]() 的小滑块
的小滑块![]() 以初速度
以初速度![]() 从
从![]() 的左端水平滑上
的左端水平滑上![]() ,随后
,随后![]() 向右运动,长木板
向右运动,长木板![]() 与平台
与平台![]() 碰撞前的瞬间,小滑块
碰撞前的瞬间,小滑块![]() 的速度大小为
的速度大小为![]() ,此时
,此时![]() 还未达到共同速度.设长木板
还未达到共同速度.设长木板![]() 与平台碰撞后立即被锁定,小滑块
与平台碰撞后立即被锁定,小滑块![]() 可视为质点,小滑块A与平台
可视为质点,小滑块A与平台![]() 之间的动摩擦因数
之间的动摩擦因数![]() 小滑块
小滑块![]() 与平台
与平台![]() 之间的动摩擦因数
之间的动摩擦因数![]() ,
,![]() ,
,![]() ,求:
,求:
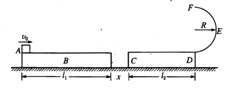
(1)长木板![]() 与平台碰撞前的瞬间,
与平台碰撞前的瞬间, ![]() 的速度大小;
的速度大小;
(2)小滑块![]() 最终停在离木板
最终停在离木板![]() 左端多远处?
左端多远处?
【答案】(1)1m/s(2)3.5m
【解析】
(1)B与平台CD碰撞前瞬间,A、B还未达到共同速度.对B,运用动能定理求B的速度大小.
(2)根据能量守恒定律求出B与平台碰撞前A相对B发生的位移,对滑块从平台C点运动到D的过程中,在到最高点的过程中运用动能定理列式,求出小物块A在半圆轨道上达到的最大高度.再对物块A过C之后在B上运动的过程使用动能定理即可求解.
(1)B与平台CD碰撞时,A、B还未达到共同速度.设B与档板碰撞前瞬间速度大小为vB,由动能定理有:
μ1mgs=![]() MvB2
MvB2
代入数据解得:vB=1m/s
(2)B与平台碰撞前A相对B发生的位移为x,根据能量守恒定律有:
μ1mgx=![]() mv02-
mv02-![]() mvA2-
mvA2-![]() MvB2
MvB2
代入数据解得:x=4.5m
即B与平台碰撞时,A恰好到达平台左端.
设A在半圆形轨道上能到达的最大高度为h,则由动能定理有:-μ2mgl2-mgh=0-![]() mvA2
mvA2
代入数据解得:h=0.5m<R
故m到达最高点后沿半圆形轨道返回.
设A到达C点时速度为vC,由动能定理有:mgh-μ2mgl2=![]() mvC2
mvC2
代入数据解得:vC=2m/s
A过C之后在B上运动的距离为l,有:-μ1mgl=-![]() mvC2
mvC2
解得:l=1m,即A最终停在离B木板左端3.5m处.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案