题目内容
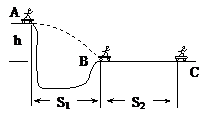
 如图所示,某滑板爱好者在离地面h=3.2m高的平台上滑行,水平离开A点后落在水平面上的B点,其水平位移X1=4m,着地时由于存在机械能损失,着地后速度大小变为v=4m/s,并以此为初速度沿水平地面滑行X2=4m后停止运动.已知人与滑板的总质量m=50kg(不计空气阻力,g取10m/s2).求:(1)人与滑板离开平台时的水平初速度大小;
如图所示,某滑板爱好者在离地面h=3.2m高的平台上滑行,水平离开A点后落在水平面上的B点,其水平位移X1=4m,着地时由于存在机械能损失,着地后速度大小变为v=4m/s,并以此为初速度沿水平地面滑行X2=4m后停止运动.已知人与滑板的总质量m=50kg(不计空气阻力,g取10m/s2).求:(1)人与滑板离开平台时的水平初速度大小;(2)人与滑板在水平地面滑行时受到的阻力大小;
(3)人与滑板着地时机械能的损失量.
分析:(1)人与滑板离开平台做平抛运动,利用平抛运动的规律,在水平和竖直两个方向上独立讨论运动规律,时间由竖直方向的高度决定,水平方向匀速运动,利用X1=v0t求出初速度大小.
(2)人与滑板在水平地面滑行时受到摩擦阻力最后停下来,由动能定理求出受到的阻力大小.
(3)根据能量守恒定律求解人与滑板着地时机械能的损失量.
(2)人与滑板在水平地面滑行时受到摩擦阻力最后停下来,由动能定理求出受到的阻力大小.
(3)根据能量守恒定律求解人与滑板着地时机械能的损失量.
解答:解:(1)从A到B过程,由平抛运动规律得:
h=
gt2
X1=v0t
则得:v0=X1
=4×
m/s=5m/s.
(2)从B到C过程,由动能定理得:
-fX2=0-
mv2
则得:f=
=
N=100N;
(3)人与滑板着地时机械能的损失量为:
△E=mgh+
m
-
mv2=50×10×3.2+
×50×52-
×50×42=1825(J);
答:
(1)人与滑板离开平台时的水平初速度大小是5m/s;
(2)人与滑板在水平地面滑行时受到的阻力大小是100N;
(3)人与滑板着地时机械能的损失量是1825J.
h=
| 1 |
| 2 |
X1=v0t
则得:v0=X1
|
|
(2)从B到C过程,由动能定理得:
-fX2=0-
| 1 |
| 2 |
则得:f=
| mv2 |
| 2X2 |
| 50×42 |
| 2×4 |
(3)人与滑板着地时机械能的损失量为:
△E=mgh+
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:
(1)人与滑板离开平台时的水平初速度大小是5m/s;
(2)人与滑板在水平地面滑行时受到的阻力大小是100N;
(3)人与滑板着地时机械能的损失量是1825J.
点评:本题注意分段讨论,水平面上的匀减速运动可以利用动能定理求出阻力,平抛段利用平抛运动规律求解.

练习册系列答案
相关题目
 如图所示,某滑板爱好者在离地h=1.8m的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移X=3m.着地时由于机械能的损失,着地后速度变为水平方向,大小为v=4m/s,并以此速度沿水平地面滑行L=8m后停止在C点.(空气阻力忽略不计)求:
如图所示,某滑板爱好者在离地h=1.8m的平台上滑行,水平离开A点后落在水平地面上的B点,其水平位移X=3m.着地时由于机械能的损失,着地后速度变为水平方向,大小为v=4m/s,并以此速度沿水平地面滑行L=8m后停止在C点.(空气阻力忽略不计)求: