题目内容
A、B两带电小球，A固定不动，B的质量为m、电荷量为q，在库仑力作用下，B由静止开始在水平面上运动.已知开始时，A、B间的距离为L，B的加速度为a，经过一段时间后，B的加速度为a/4.此时A、B间距离为多少?已知此时B的速度为v，则在此过程中电荷电势能的减少量为多少?如果A不固定，且质量为2m，电荷量为2q，则同样当B的速度为v时，A、B两个电荷的电势能减少量又为多少?
2L 
mv2 
mv2
解析:
由牛顿第二定律F=ma和库仑定律F=k
可知，小球B的加速度a∝
.设小球B的加速度为a/4时两球间的距离为s，则有
=（
）2，解得s=2L.
此过程电场力做正功，电荷的电势能减少，转化为B球的动能.则此过程中电荷电势能的减少量为ΔE=mv2.
若A不固定，释放后两球都将运动，对两球所组成的系统，合外力为零，动量守恒.设当B球的速度为v时，A球的速度为v′，则有0=mv+2mv′，此过程A、B两个电荷的电势能减少量为ΔE′=mv2+×2mv′2 ，解得ΔE′=mv2.
练习册系列答案
阅读快车系列答案
相关题目
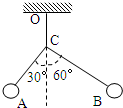A、B两带电小球，质量分别为mA、mB，用绝缘不可伸长的细线如图悬挂，静止时A、B两球处于相同高度．若B对A及A对B的库仑力分别为FA、FB，则下列判断正确的是（ ）