题目内容
A、B两带电小球，A固定不动，B的质量为m．在库仑力的作用下，B由静止开始运动．初始时，AB间的距离为d，B的加速度为a．经过一段时间后，B的加速度变为
，此时A、B间的距离应为
| a | 4 |
2d
2d
．分析：当在真空中两个点电荷，其间的库仑力与两点电荷的电量乘积成正比，与间距的平方成反比．两球在某一状态下，小球加速度与质量成反比．同一小球在不同状态下，加速度与合力成正比．
解答：解：B球仅在库仑力作用下，由静止开始运动，当间距为d时，B的加速度为a，则合力为F=ma，且F与d的平方成反比；
当B的加速度为
，此时B球的合力为F′=
，则两球间距为2d．
故答案为：2d
当B的加速度为
| a |
| 4 |
| ma |
| 4 |
故答案为：2d
点评：由库仑定律可知，在真空是必须确保电荷量不变，且电荷间距要大是能将带电量看成点来处理．同时运用牛顿第二定律来确定力与加速度的关系．
练习册系列答案
相关题目
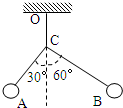A、B两带电小球，质量分别为mA、mB，用绝缘不可伸长的细线如图悬挂，静止时A、B两球处于相同高度．若B对A及A对B的库仑力分别为FA、FB，则下列判断正确的是（ ）