题目内容
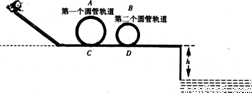
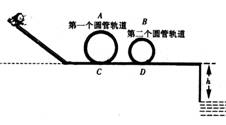
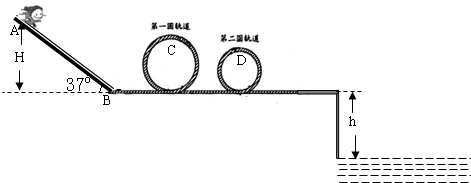
如图所示,是某公园设计的一种惊险刺激的娱乐设施,轨道除AB部分粗糙(μ=0.125)外,其余均光滑,AB斜面与水平面夹角为370.一挑战者质量为m=60kg,沿斜面轨道滑下,然后滑入第一个圆形轨道(轨道半径R=2m),不计过B点时的能量损失,根据设计要求,在最低点与最高点各放一个压力传感器,测试挑战者对轨道的压力,并通过计算机显示出来.挑战者到达C处时刚好对轨道无压力,又经过水平轨道滑入第二个圆形轨道(轨道半径r=1.6m),然后从平台上飞入水池内,水面离轨道的距离为h=5m.g取10m/s2,人在运动全过程中可视为质点.求:
(1)在第二个圆形轨道的最高点D处挑战者对轨道的压力大小.
(2)挑战者若能完成上述过程,则他应从离水平轨道多高的地方开始下滑.
(3)挑战者入水时的速度大小是多少?方向如何?
(1)在第二个圆形轨道的最高点D处挑战者对轨道的压力大小.
(2)挑战者若能完成上述过程,则他应从离水平轨道多高的地方开始下滑.
(3)挑战者入水时的速度大小是多少?方向如何?

分析:(1)由题,挑战者到达C处时刚好对轨道无压力,由重力提供向心力,求出C点的速度.由C到D的过程中,只有重力做功mg(2R-2r),根据动能定理求出挑战者到达D处的速度,由牛顿运动定律求解D处挑战者对轨道的压力大小.
(2)挑战者从开始下滑到C点的过程中,重力做功mg(H-2R),摩擦力做功-μmgcos37°?
,根据动能定理求出高度H.
(3)挑战者从C点到落水过程中,重力做功mg(2R+h),根据动能定理求解挑战者入水时的速度大小.研究B到C的过程求出B点的速度.挑战者离开水平轨道后做平抛运动的初速度等于B点的速度,由速度的分解可求解挑战者入水时的速度.
(2)挑战者从开始下滑到C点的过程中,重力做功mg(H-2R),摩擦力做功-μmgcos37°?
| H |
| sin37° |
(3)挑战者从C点到落水过程中,重力做功mg(2R+h),根据动能定理求解挑战者入水时的速度大小.研究B到C的过程求出B点的速度.挑战者离开水平轨道后做平抛运动的初速度等于B点的速度,由速度的分解可求解挑战者入水时的速度.
解答:解:
(1)在C点无压力则 mg=m
由C到D动能定理得
mg(2R-2r)=
m
-
m
D点牛顿第二定律得 N+mg=m
联立方程得 N=750N
由牛顿第三定律得到:人对轨道的压力N′=750N
(2)挑战者从开始下滑到C点的过程中,由动能定理得
mg(H-2R)-μmgcos37°?
=
m
-0
代入解得 H=6m
(3)挑战者从C点到落水过程中,由动能定理得
mg(2R+h)=
mv2
代入解得 v=10
m/s
B到C动能定理得-mg?2R=
m
-
m
得vB=10m/s
挑战者离开水平轨道后后做平抛运动.水平方向速度大小等于vB不变.由数学知识可知,挑战者入水时的速度方向与水平方向的夹角为45°.
(1)在C点无压力则 mg=m
| ||
| R |
由C到D动能定理得
mg(2R-2r)=
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
| v | 2 C |
D点牛顿第二定律得 N+mg=m
| ||
| r |
联立方程得 N=750N
由牛顿第三定律得到:人对轨道的压力N′=750N
(2)挑战者从开始下滑到C点的过程中,由动能定理得
mg(H-2R)-μmgcos37°?
| H |
| sin37° |
| 1 |
| 2 |
| v | 2 C |
代入解得 H=6m
(3)挑战者从C点到落水过程中,由动能定理得
mg(2R+h)=
| 1 |
| 2 |
代入解得 v=10
| 2 |
B到C动能定理得-mg?2R=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
得vB=10m/s
挑战者离开水平轨道后后做平抛运动.水平方向速度大小等于vB不变.由数学知识可知,挑战者入水时的速度方向与水平方向的夹角为45°.
点评:本题是多过程问题,应用动能定理时要灵活选择研究的过程.本题研究物体在斜面上运动的过程时,也可以采用牛顿第二定律和运动学公式结合的方法进行处理.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
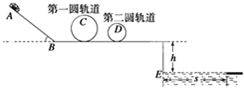 如图所示,是某公园设计的一种游乐设施,所有轨道均光滑,AB面与水平面成一定夹角.一无动力小滑车质量为m=10kg,沿斜面轨道由静止滑下,然后滑入第一个圆形轨道内侧,其轨道半径R=2.5m,不计过B点的能量损失,根据设计要求,在圆轨道最低点与最高点各放一个压力传感器,测试小滑车对轨道的压力,并通过计算机显示出来.小滑车到达第一圆轨道最高点C处时刚好对轨道无压力,又经过水平轨道滑入第二个圆形轨道内侧,其轨道半径r=l.5m,然后从水平轨道上飞入水池内,水面离水平轨道的距离为h=5m.g取10m/s2,小滑车在运动全过程中可视为质点.求:
如图所示,是某公园设计的一种游乐设施,所有轨道均光滑,AB面与水平面成一定夹角.一无动力小滑车质量为m=10kg,沿斜面轨道由静止滑下,然后滑入第一个圆形轨道内侧,其轨道半径R=2.5m,不计过B点的能量损失,根据设计要求,在圆轨道最低点与最高点各放一个压力传感器,测试小滑车对轨道的压力,并通过计算机显示出来.小滑车到达第一圆轨道最高点C处时刚好对轨道无压力,又经过水平轨道滑入第二个圆形轨道内侧,其轨道半径r=l.5m,然后从水平轨道上飞入水池内,水面离水平轨道的距离为h=5m.g取10m/s2,小滑车在运动全过程中可视为质点.求: