题目内容
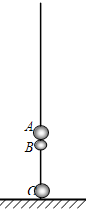 如图所示,均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘细线上,A与B紧靠在一起(但不粘连),C紧贴着绝缘地板,质量分别为MA=2.32kg,MB=0.20kg,MC=2.00kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5c,qC=+7.0×10-5c,且电量都保持不变,开始时三个物体均静止.现给物体A施加一个竖直向上的力F,若使A由静止开始向上作加速度大小为a=4.0m/s2的匀加速直线运动,则开始需给物体A施加一个竖直向上的变力F,经时间t 后,F变为恒力.已知g=10m/s2,静电力恒量k=9×109N?m2/c2,求:
如图所示,均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘细线上,A与B紧靠在一起(但不粘连),C紧贴着绝缘地板,质量分别为MA=2.32kg,MB=0.20kg,MC=2.00kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5c,qC=+7.0×10-5c,且电量都保持不变,开始时三个物体均静止.现给物体A施加一个竖直向上的力F,若使A由静止开始向上作加速度大小为a=4.0m/s2的匀加速直线运动,则开始需给物体A施加一个竖直向上的变力F,经时间t 后,F变为恒力.已知g=10m/s2,静电力恒量k=9×109N?m2/c2,求:(1)静止时B与C之间的距离;
(2)时间t的大小;
(3)在时间t内,若变力F做的功WF=53.36J,则B所受的电场力对B做的功为多大?
分析:(1)研究开始静止状态,对AB整体,合力为零,由平衡条件和库仑定律求解开始时BC间的距离x1;
(2)给A施加力F后,AB沿斜面向上做匀加速运动,当AB分离之后F成为恒力,当两者之间弹力恰好为零时,根据牛顿第二定律得到BC距离,由运动学位移公式求出时间t;
(3)在时间t内,对AB运用动能定理求出电场力做功,即可求得电场力对B做的功.
(2)给A施加力F后,AB沿斜面向上做匀加速运动,当AB分离之后F成为恒力,当两者之间弹力恰好为零时,根据牛顿第二定律得到BC距离,由运动学位移公式求出时间t;
(3)在时间t内,对AB运用动能定理求出电场力做功,即可求得电场力对B做的功.
解答:解:(1)开始时A、B处于平衡状态,设BC之间的距离为x1,则
(MA+MB)g=k
,代入数据可得:x1=1.0m.
(2)经时间t,F变为恒力.A、B恰好分离,A、B间无相互作用,设BC之间的距离为x2则
k
-MBg=MBa,代入数据可得:x2=3.0m.
因为x2-x1=
at2,代入数据可得t=1s.
(3)以AB为系统,由动能定理可得
WF+W电-(MA+MB)g(x2-x1)=
(MA+MB)v2
而v=at
代入数据可得:W电=17.2J.
答:(1)静止时B与C之间的距离为1m;
(2)时间t为1s;
(3)B所受的电场力对B做的功为17.2J.
(MA+MB)g=k
| qBqC |
| x12 |
(2)经时间t,F变为恒力.A、B恰好分离,A、B间无相互作用,设BC之间的距离为x2则
k
| qBqC |
| x22 |
因为x2-x1=
| 1 |
| 2 |
(3)以AB为系统,由动能定理可得
WF+W电-(MA+MB)g(x2-x1)=
| 1 |
| 2 |
而v=at
代入数据可得:W电=17.2J.
答:(1)静止时B与C之间的距离为1m;
(2)时间t为1s;
(3)B所受的电场力对B做的功为17.2J.
点评:本题的解题关键是抓住AB刚分离时弹力为零,运用牛顿第二定律BC间的距离,要善于挖掘隐含的临界状态,把握临界条件进行分析.

练习册系列答案
相关题目
 [物理─选修3-5]
[物理─选修3-5] (2007?湖北模拟)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球E拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,若取D点的电势为零,试求:
(2007?湖北模拟)如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方.现在把小球E拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v.已知静电力常量为k,若取D点的电势为零,试求: 如图所示,质量为M=1kg的平板小车上放置着ml=3kg,m2=2kg的物块,两物块与小车间的动摩擦因数为μ=0.5.两物块间夹有一压缩轻质弹簧,物块间有张紧的轻绳相连.小车右端有与m2相连的锁定开关,现已锁定.水平地面光滑,物块均可视为质点.现将轻绳烧断,若己知m1相对小车滑过0.6m时从车上脱落,此时小车以速度v0=2m/s向右运动,当小车第一次与墙壁碰撞瞬间锁定开关打开.设小车与墙壁碰撞前后速度大小不变,碰撞时间极短,小车足够长.(g=10m/s2)求:
如图所示,质量为M=1kg的平板小车上放置着ml=3kg,m2=2kg的物块,两物块与小车间的动摩擦因数为μ=0.5.两物块间夹有一压缩轻质弹簧,物块间有张紧的轻绳相连.小车右端有与m2相连的锁定开关,现已锁定.水平地面光滑,物块均可视为质点.现将轻绳烧断,若己知m1相对小车滑过0.6m时从车上脱落,此时小车以速度v0=2m/s向右运动,当小车第一次与墙壁碰撞瞬间锁定开关打开.设小车与墙壁碰撞前后速度大小不变,碰撞时间极短,小车足够长.(g=10m/s2)求: 在长为2L的绝缘轻质细杆的两端各连接一个质量均为m的带电小球A和B(可视为质点,也不考虑二者间的相互作用力),A球带正电、电荷量为+2q,B球带负电.电荷量为-3q.现把A和B组成的带电系统锁定在光滑绝缘的水平面上,并让A处于如图所示的有界匀强电场区域MPQN内.已知虚线MP是细杆的中垂线,MP和NQ的距离为4L,匀强电场的场强大小为E,方向水平向右.现取消对A、B的锁定,让它们从静止开始运动.(忽略小球运动中所产生的磁场造成的影响)
在长为2L的绝缘轻质细杆的两端各连接一个质量均为m的带电小球A和B(可视为质点,也不考虑二者间的相互作用力),A球带正电、电荷量为+2q,B球带负电.电荷量为-3q.现把A和B组成的带电系统锁定在光滑绝缘的水平面上,并让A处于如图所示的有界匀强电场区域MPQN内.已知虚线MP是细杆的中垂线,MP和NQ的距离为4L,匀强电场的场强大小为E,方向水平向右.现取消对A、B的锁定,让它们从静止开始运动.(忽略小球运动中所产生的磁场造成的影响) [物理-选修3-5]
[物理-选修3-5]