题目内容
 [物理-选修3-5]
[物理-选修3-5](1)北京时间20l1年3月11日在日本海域发生强烈地震,强震引发了福岛核电站危机.下列关于核裂变和核辐射的方程中书写正确的是
C
C
:A.92235U+01n→56141Ba+3692Kr+1001n B.94235Pu→92235U+24He C.55137 Cs→56137Ba+-10e D.55121I→54131Ce+-10e
(2)如图所示,光滑水平面上放置质量均为M=2kg的甲、乙两辆小车 两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离).其中甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.5.一根通过细线拴着而被压缩的轻质弹簧固定在甲 车的左端,质量为m=l kg的滑块P(可视为质点)与弹簧的右端接触但不相连,弹簧原长小于甲车长度,整个系统处于静止.现剪断细线,已知滑块P刚滑上乙车时,滑块相对地面的速度为ν1=4m/s,且滑块P最终滑有滑离乙车,求滑块P在乙车上滑行的距离.
分析:(1)核反应中要求电荷数守恒、质量数守恒;分析以上两点可知书写是否正确;
(2)在P滑动过程中分别对P与甲、P与乙由动量守恒及动能定理可求得滑块在乙车上滑行的距离.
(2)在P滑动过程中分别对P与甲、P与乙由动量守恒及动能定理可求得滑块在乙车上滑行的距离.
解答:解:(1)由电荷数守恒及质量数守恒可知,A、B、D错误,C正确;
故选BCD.
(2)设滑块P刚滑上乙车时,两车的速度为v2,对甲车、乙车和滑块来说有:
mv1-2Mv2=0
解得v2=1m/s; 方向向左;
设滑块在乙车上滑行的过程中,乙车对地滑行的距离为s,滑块P在乙车上滑行的距离为L,滑块P和乙车达到的共同速度为v.对滑块P和乙车来说:
mv1-Mv2=(m+M)v
解得v=
m/s
研究乙车,由动能定理可知
μmgs=
Mv2-
Mv22
研究滑块P,根据动能定理可得
-μmg(s+L)=
mv2-
mv12
联立以上两式可得:
μmgL=
mv12+
Mv22-
(m+M)v2
将题中数据代入得:L=
m
答:滑块P在乙车上滑行的距离为
m.
故选BCD.
(2)设滑块P刚滑上乙车时,两车的速度为v2,对甲车、乙车和滑块来说有:
mv1-2Mv2=0
解得v2=1m/s; 方向向左;
设滑块在乙车上滑行的过程中,乙车对地滑行的距离为s,滑块P在乙车上滑行的距离为L,滑块P和乙车达到的共同速度为v.对滑块P和乙车来说:
mv1-Mv2=(m+M)v
解得v=
| 2 |
| 3 |
研究乙车,由动能定理可知
μmgs=
| 1 |
| 2 |
| 1 |
| 2 |
研究滑块P,根据动能定理可得
-μmg(s+L)=
| 1 |
| 2 |
| 1 |
| 2 |
联立以上两式可得:
μmgL=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
将题中数据代入得:L=
| 5 |
| 3 |
答:滑块P在乙车上滑行的距离为
| 5 |
| 3 |
点评:(1)本题考查3-5的内容,3-5中应重点把握动量守恒及原子物理中的核反应规律,一般来说动量守恒为简单的单向动量守恒,结合能量关系可得出正确结果.
(2)本题考察了动量守恒.机械能守恒和能量的转化与守恒.
应用动量守恒定律解题要注意“四性”,①、系统性:应明确研究对象是一个系统,同时确保系统的初、末状态的动量相等.②、矢量性:系统在作用前后,各物体动量的矢量和保持不变,当各速度在同一条直线上时,选定正方向,将矢量运算转化为代数运算.③、同时性:作用前系统各部分的速度应为同一时刻的速度,作用后系统各部分的速度也应为同一时刻的速度.④、同系性:列动量守恒的方程时,所有动量都必须相对同一惯性参照系.
机械能守恒的条件是只有重力(或弹簧的弹力)做功,并只发生动能和势能的转化.
(2)本题考察了动量守恒.机械能守恒和能量的转化与守恒.
应用动量守恒定律解题要注意“四性”,①、系统性:应明确研究对象是一个系统,同时确保系统的初、末状态的动量相等.②、矢量性:系统在作用前后,各物体动量的矢量和保持不变,当各速度在同一条直线上时,选定正方向,将矢量运算转化为代数运算.③、同时性:作用前系统各部分的速度应为同一时刻的速度,作用后系统各部分的速度也应为同一时刻的速度.④、同系性:列动量守恒的方程时,所有动量都必须相对同一惯性参照系.
机械能守恒的条件是只有重力(或弹簧的弹力)做功,并只发生动能和势能的转化.

练习册系列答案
相关题目
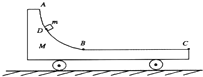 (2)如图,小车质量为M=2.0kg,带有光滑的圆弧轨道AB和粗糙的水平轨道BC,一小物块(可视为质点)质量为m=0.5kg,与轨道BC的动摩擦因数为μ=0.10,BC部分总长度为L=0.80m.重力加速度g取10m/s2.
(2)如图,小车质量为M=2.0kg,带有光滑的圆弧轨道AB和粗糙的水平轨道BC,一小物块(可视为质点)质量为m=0.5kg,与轨道BC的动摩擦因数为μ=0.10,BC部分总长度为L=0.80m.重力加速度g取10m/s2. 物理--选修3-5
物理--选修3-5 (物理-选修3-5)
(物理-选修3-5)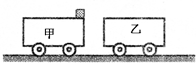
 (2011?长春二模)[物理--选修3-5]
(2011?长春二模)[物理--选修3-5]