��Ŀ����
����Ŀ����ͼ��ʾ���ڴֲ�ˮƽ������һ����ΪM=2 kg����⻬��б���壬б��������=37������б�����������Ϊd=2.4 m����һ�̶��ϰ���Q����һ����Ϊm=0.2 kg��С��飨����Ϊ�ʵ㣩��һ�������������쳤��ϵס������һ�˹̶���б����Ķ��ˡ��ָ�б����ʩ��һ��ˮƽ���������F��ʹб�����С�������Ի�����һ���������ȼ����˶�����б���嵽���ϰ���Q������ײ��б�����������ϰ���Q��������֪б����������Ķ�Ħ������Ϊ��=0.5���������ٶ�g=10 m/s2���軬��Ħ�����������Ħ��������
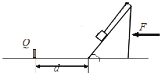
��1��ˮƽ����F�����ֵ��
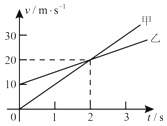
��2���������ˮƽ����������б�����ϣ�б���屻�ϰ���Q������С���������ǣ��������Բ���˶�����ֱ��ߵ㣬�����ij���Ӧ���������.��������������λ��Ч���֣�
���𰸡���1��27.5N��2��L��0.31m
��������
��1���������֪����F���ʱ��С��鲻�����ӵ���������С���Ϊ�о�����
mgtan��=ma
�������ݽ�ã�a=7.5m/s2
��С����б������Ϊ�о�����F�C�̣�M+m��g��M+m��a
��ã� F=27.5N
��2����б������ٹ����У����ٶ�λ�ƹ�ϵ��2ad=v2 �� v=6m/s
��С����뿪б��˲����ٶ�Ϊv1����v1=vsin��=3.6m/s
С���պ�ͨ����ߵ㣬�����ij���ΪL
С�������ߵ�ʱ��![]()
�ɻ�е���غ㶨�ɵ�![]()
���L=0.31m
����LӦ����L��0.31m