题目内容
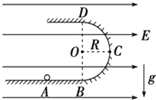
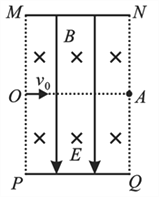
【题目】如图所示，长均为d的两正对平行金属板MN、PQ水平放置，板间距离为2d，板间有正交的竖直向下的匀强电场和垂直纸面向里的匀强磁场，一质量为
的带电粒子从MP的中点O垂直于电场和磁场方向以v0射入，恰沿直线从NQ的中点A射出；若撤去电场，则粒子从M点射出（粒子重力不计）。以下说法正确的是
A. 该粒子带正电
B. 若撤去电场,则该粒子运动时间为原来的
倍
C. 若撤去磁场，则该粒子在运动过程中电势能增加
D. 若撤去磁场，则粒子射出时的速度大小为
v0
【答案】AD
【解析】撤去电场，粒子从M点射出，粒子刚射入磁场时所受洛伦兹力竖直向上，由左手定则知粒子带正电荷，故A正确；电磁场共存时，粒子运动的时间
；撤去电场后，粒子在磁场中做匀速圆周运动的时间：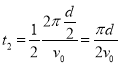 
，则该粒子运动时间为原来的
，选项B错误；
设粒子的质量为m，带电量为q，粒子射入电磁场时的速度为v0，则粒子沿直线通过场区时：Bqv0=Eq，撤去电场后，在洛仑兹力的作用下，粒子做圆周运动，由几何知识知：r=
d，洛仑兹力提供向心力，由牛顿第二定律得： 
；撤去磁场，粒子做类平抛运动，粒子的加速庶a，穿越电场所用时间为t，水平方向：d=v0t，加速度： 
，竖直分位移：y=
at2，解得：y=d，设末速度为v，由动能定理知： 
mv2-
mv02=Eqd，解得：v=
v0，故D正确；故选AD．
练习册系列答案
相关题目
