题目内容
如图所示，轻绳OA一端系于天花板上，与竖直方向的夹角为30°，水平轻绳OB的一端系于竖直墙上，O点挂一重物．重物重力300N，此时绳OA、OB的拉力是多大？（结果保留三位有效数字）分析：以结点O为研究对象，分析受力情况，结点平衡，合力为零，由平衡条件求解绳OA、OB的拉力．
解答：解：设OA绳的拉力为F1，OB绳的拉力为F2．分析结点O受力情况：重物的拉力T，绳OA的拉力F1和OB的拉力F2．由结点O平衡可知：
F1cosθ=T=mg
将θ=30°，mg=300N代入，得：F1=
=200
N≈346N
F2=F1sin30°=173N
答：绳OA的拉力是346N、OB的拉力是173N．
F1cosθ=T=mg
将θ=30°，mg=300N代入，得：F1=
| mg |
| cos30° |
| 3 |
F2=F1sin30°=173N
答：绳OA的拉力是346N、OB的拉力是173N．
点评：本题绳系系统平衡问题，通常以结点O为研究对象，根据平衡条件进行研究．
练习册系列答案
相关题目
如图所示，轻绳OA与水平方向夹角为30°，轻绳OB与OA相互垂直，轻绳OC下端悬挂一质量为m的物体．重力加速度为g．则（ ）
如图所示，轻绳OA一端系于天花板上与竖直方向的夹角为30°，轻绳OB一端系于墙上，O点挂一重为30N的物体，当OB绳呈水平时，OA，OB两绳各受多大的拉力．
如图所示，轻绳OA一端系在天花板上，与竖直线夹角为37°，轻绳OB水平，一端系在墙上，O点处挂一重为40N的物体．绳AO拉力为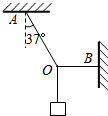
如图所示，轻绳OA一端系于天花板上，与竖直方向的夹角为37°，水平轻绳OB的一端系于竖直墙上，O点挂一重物．重物重力为240N，此时绳OA、OB的拉力是多大？（取重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8）