题目内容
11. 如图所示,一带正电的摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,此时小球恰好与水平面相切,然后沿粗糙水平面由D点向右做匀减速运动,到达小孔A进入半径R=0.1m的竖直放置的光滑圆弧轨道.圆轨道处在一个方向水平向右的有界匀强电场中,电场边界MN、PQ与圆轨道相切.若已知摆线长L=1m,θ=60°,D点与小孔A的水平距离s=2m,小球质量m=0.1kg,小球所受电场力为其重力的$\frac{3}{4}$倍,g取10m/s2.求:
如图所示,一带正电的摆球从图中的C位置由静止开始摆下,摆到最低点D处,摆线刚好被拉断,此时小球恰好与水平面相切,然后沿粗糙水平面由D点向右做匀减速运动,到达小孔A进入半径R=0.1m的竖直放置的光滑圆弧轨道.圆轨道处在一个方向水平向右的有界匀强电场中,电场边界MN、PQ与圆轨道相切.若已知摆线长L=1m,θ=60°,D点与小孔A的水平距离s=2m,小球质量m=0.1kg,小球所受电场力为其重力的$\frac{3}{4}$倍,g取10m/s2.求:(1)摆线所受的最大拉力;
(2)要使摆球进入圆轨道后能做完整的圆周运动,水平面摩擦因数μ的大小应满足什么条件?(计算结果保留2位有效数字,sin37°=0.6,cos37°=0.8)
分析 (1)摆球摆到D点时,摆线的拉力最大,根据机械能守恒定律求出摆球摆到D点时速度,由牛顿第二定律求出摆线的最大拉力.
(2)根据重力和电场力的合力得出等效重力场,要使摆球能进入圆轨道,并且不脱离轨道,要使摆球能进入圆轨道,恰好到达轨道等效最高点,就刚好不脱离轨道,在等效最高点时,由等效重力提供向心力,由牛顿第二定律求出此时小球的速度,对从D到轨道最高点的过程,运用动能定理求解动摩擦因数的最小值,即可得到μ的范围.
解答 解:(1)当摆球由C到D运动,机械能守恒,则得:mg(L-Lcosθ)=$\frac{1}{2}m{v}_{D}^{2}$
在D点,由牛顿第二定律可得:Fm-mg=$\frac{m{v}_{D}^{2}}{L}$
联立可得:摆线的最大拉力为 Fm=2mg=2N
(2)等效重力mg'=$\sqrt{(mg)^{2}+(Eq)^{2}}$=$\frac{5}{4}$mg;
方向与竖直方向夹角为tanα=$\frac{Eq}{mg}$=$\frac{3}{4}$;
则α=37°;
设等效最高点为E,则有:mg'=m$\frac{{v}_{E}^{2}}{R}$;
对摆球由动能定理可得:
-μmgs+qER(1-sinα)-mg(1+cosα)=$\frac{1}{2}$mvE2-$\frac{1}{2}$mvD2
要使小球能过圆轨道的最高点则不会脱离轨道,在圆周的最高点由牛顿第二定律可得:$mg=m\frac{v^2}{R}$
由动能定理可得:-μmgs-2mgR+qER=$\frac{1}{2}$mv2-$\frac{1}{2}$mvD2
解得:μ=0.125
答:(1)摆线能承受的最大拉力为2N;
(2)使摆球进入圆轨道后能做完整的圆周运动,水平面摩擦因数μ的大小应满足μ≤0.125.
点评 本题考查机械能守恒定律及动能定理、向心力公式等;关键是要全面分析不能漏解,要知道摆球能进入圆轨道不脱离轨道应是恰好通过等效最高点;然后再根据牛顿第二定律、机械能守恒和动能定理结合进行求解.

 阅读快车系列答案
阅读快车系列答案| A. | 在真空中的波长较短 | |
| B. | 在玻璃中传播的速度较大 | |
| C. | 在玻璃中传播时,玻璃对其折射率较大 | |
| D. | 其在空气中传播速度大 |
| A. | 火箭的发射 | B. | 宇宙飞船绕地球的运动 | ||
| C. | 宇宙探测器 | D. | 微观粒子的运动 |
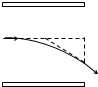 如图,一束由质子、氘核和氚核组成的粒子流,从相同位置沿垂直于场强的方向射入由平行板电容器形成的同一个匀强电场中.若所有粒子均能射出电场,不计粒子的重力及粒子间的相互作用力,关于粒子的运动情况,下列说法正确的是( )
如图,一束由质子、氘核和氚核组成的粒子流,从相同位置沿垂直于场强的方向射入由平行板电容器形成的同一个匀强电场中.若所有粒子均能射出电场,不计粒子的重力及粒子间的相互作用力,关于粒子的运动情况,下列说法正确的是( )| A. | 若粒子的运动轨迹相同,说明它们具有相同的初动能 | |
| B. | 比荷大的粒子,在射出电场时,其速度偏向角一定大 | |
| C. | 若粒子在电场中的运动时间相等,则它们的初速度一定相等 | |
| D. | 在电场中运动时间越长的粒子,电场力对它做的功越多 |
 如图所示的实验装置中,充电后的平行板电容器的A极板与灵敏静电计的金属球相接,极板B和静电计外壳均接地.利用该装置研究平行板电容器的电容与哪些因素有关,下列叙述符合观察结果的是( )
如图所示的实验装置中,充电后的平行板电容器的A极板与灵敏静电计的金属球相接,极板B和静电计外壳均接地.利用该装置研究平行板电容器的电容与哪些因素有关,下列叙述符合观察结果的是( )| A. | 将B板向左平移,静电计指针偏角变大 | |
| B. | 将B板向上平移,静电计指针偏角变小 | |
| C. | 在A、B板间插入一块绝缘介质板,静电计指针偏角变大 | |
| D. | 在A、B板间插入一块较厚金属板,静电计指针偏角变小 |
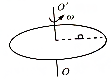 如图所示,水平圆盘绕竖直转轴OO′匀速转动,质量为m的小物体(可视为质点)在圆盘上距转轴OO′距离r处相对圆盘静止,小物体与圆盘动摩擦因数为μ.设最大静摩擦力与滑动摩擦力大小相等,重力加速度为g,求:
如图所示,水平圆盘绕竖直转轴OO′匀速转动,质量为m的小物体(可视为质点)在圆盘上距转轴OO′距离r处相对圆盘静止,小物体与圆盘动摩擦因数为μ.设最大静摩擦力与滑动摩擦力大小相等,重力加速度为g,求: