题目内容
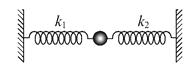
【题目】在光滑绝缘的水平面上，存在平行于水平面向右的匀强电场，电场强度为E，水平面上放置两个静止，且均可看做质点的小球A和B，两小球质量均为m，A球带电荷量为+Q，B球不带电，A、B连线与电场线平行，开始时两球相距L，在电场力作用下A球与B球发生对心弹性碰撞，设碰撞过程中，A、B两球间无电量转移。
（1）第一次碰撞结束瞬间A.B两球的速度各为多大？
（2）从开始到即将发生第二次碰到这段过程中电场力做了多少功？
（3）从开始即将发生第二次碰撞这段过程中，若要求A在运动过程中对桌面始终无压力且刚好不离开水平桌面（
时刻除外），可以在水平面内加一与电场正交的磁场，请写出磁场B与时间t的函数关系。
【答案】（1）0， 
（2）5QEL（3）从A开始运动到发生第一次碰撞：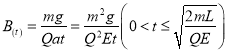 
从第一次碰撞到发生第二次碰撞：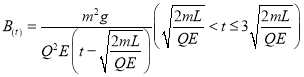 
【解析】（1）A球的加速度
，碰前A的速度
；碰前B的速度
设碰后A、B球速度分别为
、
，两球发生碰撞时，由动量守恒和能量守恒定律有：
， 
所以B碰撞后交换速度： 
， 
（2）设A球开始运动时为计时零点，即
，A、B球发生第一次、第二次的碰撞时刻分别为
、
；由匀变速速度公式有： 
第一次碰后，经
时间A、B两球发生第二次碰撞，设碰前瞬间A、B两球速度分别为
和
，由位移关系有： 
，得到： 
； 
由功能关系可得： 
（另解：两个过程A球发生的位移分别为
、
， 
，由匀变速规律推论
，根据电场力做功公式有： 
）
（3）对A球由平衡条件得到： 
， 
， 
从A开始运动到发生第一次碰撞：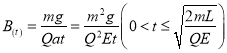 
从第一次碰撞到发生第二次碰撞：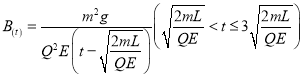 
练习册系列答案
名校课堂系列答案
相关题目
