题目内容
物理-选修3-5
(1)在匀强磁场里有一个原来静止的放射性碳14,它所放射的粒子与反冲核的径迹是两个相切的圆.圆的直径比为7:1,碳14的衰变方程是:
A.
C→
He+
Be
B.
C→
e+
B
C.
C→
e+
N
D.
C→
H+
B
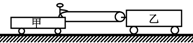
(2)如图甲所示,-根轻质弹簧的两端分别与质量为m1和m2的两个物块A、B相连接,并静止在光滑的水平面上.t=0时刻,A的速度方向水平向右,大小为3m/s,两个物块的速度随时间变化的规律如图乙所示.
根据图象提供的信息求:
①两物块的质量之比;
②在t2时刻A与B的动量之比.
(1)在匀强磁场里有一个原来静止的放射性碳14,它所放射的粒子与反冲核的径迹是两个相切的圆.圆的直径比为7:1,碳14的衰变方程是:
A.
14 6 |
4 2 |
10 4 |
B.
14 6 |
0 -1 |
14 5 |
C.
14 6 |
0 -1 |
14 7 |
D.
14 6 |
2 1 |
12 5 |
(2)如图甲所示,-根轻质弹簧的两端分别与质量为m1和m2的两个物块A、B相连接,并静止在光滑的水平面上.t=0时刻,A的速度方向水平向右,大小为3m/s,两个物块的速度随时间变化的规律如图乙所示.

根据图象提供的信息求:
①两物块的质量之比;
②在t2时刻A与B的动量之比.
分析:(1)根据洛伦兹力提供向心力列式求解出电荷之比即可;
(2)①A、B组成的系统动量守恒定律,根据守恒定律列式求解即可;、
②根据动量的定义列式求解即可.
(2)①A、B组成的系统动量守恒定律,根据守恒定律列式求解即可;、
②根据动量的定义列式求解即可.
解答:解:(1)原来静止的放射性碳14,它所放射的粒子与反冲核的总动量守恒,故放射的粒子与反冲核的动量等大、反向;
根据洛伦兹力提供向心力,得到轨道半径r=
,动量和磁感应强度相同,故半径与电量成反比,故电量之比为7:1;
故选C.
(2)①对A、B组成的系统由动量守恒定律得m1v0=(m1+m2)v1
解得:
=
②在t2时刻
=
=-
故答案为:
,-
.
根据洛伦兹力提供向心力,得到轨道半径r=
| mv |
| qB |
故选C.
(2)①对A、B组成的系统由动量守恒定律得m1v0=(m1+m2)v1
解得:
| m1 |
| m2 |
| 1 |
| 2 |
②在t2时刻
| PA |
| PB |
| m1vA |
| m2vB |
| 1 |
| 4 |
故答案为:
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题两问都是要根据动量守恒定律列式求解,其中第一问还要结合洛伦兹力提供向心力列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 [物理--选修3-5]
[物理--选修3-5] [物理-选修3-5]
[物理-选修3-5]
 [物理--选修3-5]
[物理--选修3-5]