题目内容
(14分)、传送带和水平面的夹角为37°,完全相同的两轮和皮带的切点A、B间的距离为24m, B点右侧(B点在场的边缘)有一上下无限宽左右边距为d的正交匀强电场和匀强磁场,电场方向竖直向上,匀强磁场垂直于纸面向里,磁感应强度B=103T.传送带在电机带动下,以4m/s速度顺时针匀速运转,现将质量为m=0.1kg,电量q=+10-2C的物体(可视为质点)轻放于传送带的A点,已知物体和传送带间的摩擦系数为μ=0.8,物体在运动过程中电量不变,重力加速度取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)物体从A点传送到B点的时间?
(2)若物体从B点进入混合场后做匀速圆周运动,则所加的电场强度的大小E应为多少?物体仍然从混合场的左边界出混合场,则场的右边界距B点的水平距离d至少等于多少?
11s 0.016m
解析试题分析:物体在斜面上做加速运动,由牛顿第二定律有
μmgcos370-mgsin37°=ma
得a=μmgcos37°-gsin37° (1分)
a=0.4m/s2 (1分)
物体做匀加速运动到与传送带有相同速度,有v=at1
t1=10s (1分)
物体运动位移为x= at2 (1分)
at2 (1分)
得x=20m (1分)
物体继续与传送带以相同速度匀速运动,有
LAB-X=vt2 (1分)
所以t2=1s (1分)
物体在传送带上运动总时间t=t1+t2=11s (1分)
物体在混合场中做匀速圆周运动,有gE=mg (1分)
得E=100N/C (1分)
qvB=m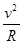 1分 R=
1分 R=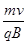 =0.04m(1分)
=0.04m(1分)
物体离开混合场有sin370= (1分)
(1分)
d=0.016m (1 分)
考点:本题考查牛顿定律应用、带电粒子在电场磁场中运动。

 名校课堂系列答案
名校课堂系列答案


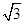 ×104V/m。一带正电的粒子(不计重力),其比荷q/m=1.0×104C/kg,从A板静止出发,经过加速电压(电压可调)加速后从坐标原点O沿x轴正方向射入磁场B1。
×104V/m。一带正电的粒子(不计重力),其比荷q/m=1.0×104C/kg,从A板静止出发,经过加速电压(电压可调)加速后从坐标原点O沿x轴正方向射入磁场B1。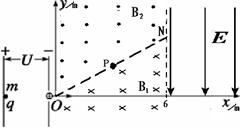
 )的A点静止释放。
)的A点静止释放。

 倍。将珠子从环最低位置A点静止释放,求:
倍。将珠子从环最低位置A点静止释放,求: