题目内容
如图所示的空间分为Ⅰ、Ⅱ、Ⅲ三个区域,各边界面相互平行,Ⅰ区域存在匀强电场,电场强度E=1.0×104V/m,方向垂直边界面向右.Ⅱ、Ⅲ区域存在匀强磁场,磁场的方向分别为垂直纸面向外和垂直纸面向里,磁感应强度分别为B1=2.0T、B2=4.0T.三个区域宽度分别为d1=5.0m、d2= d3=6.25m,一质量m=1.0×10-8kg、电荷量q=1.6×10-6C的粒子从O点由静止释放,粒子的重力忽略不计.试求:
⑴粒子离开Ⅰ区域时的速度大小v;
⑵粒子在Ⅱ区域内运动的时间t;
⑶粒子离开Ⅲ区域时速度与边界面的夹角α.
(1) v=4.0×103m/s (2)  (3) α=60°
(3) α=60°
解析试题分析:⑴粒子在电场中做匀加速直线运动,
由动能定理有: 2分
2分
解得 v=4.0×103m/s 1分
⑵设粒子在磁场B1中做匀速圆周运动的半径为r,则 1分
1分
解得 r=12.5m 1分
设在Ⅱ区内圆周运动的圆心角为θ,则 1分
1分
解得 θ=30° 1分
粒子在Ⅱ区运动周期 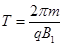 1分
1分
粒子在Ⅱ区运动时间  1分 解得
1分 解得  1分
1分
⑶设粒子在Ⅲ区做圆周运动道半径为R,则  1分
1分
解得 R="6.25m" 1分
粒子运动轨迹如图所示,由几何关系可知 为等边三角形 1分
为等边三角形 1分
粒子离开Ⅲ区域时速度与边界面的夹角 α=60° 2分
考点:带电粒子在匀强磁场中的运动;牛顿第二定律;向心力;动能定理的应用;带电粒子在匀强电场中的运动

练习册系列答案
相关题目


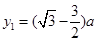 平面直角坐标系中,直线
平面直角坐标系中,直线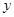 与
与 轴成30°角,
轴成30°角, 点的坐标为(
点的坐标为( ,0),在
,0),在 之间的区域内,存在垂直于
之间的区域内,存在垂直于 平面向里磁感强度为
平面向里磁感强度为 的匀强磁场.均匀分布的电子束以相同的速度
的匀强磁场.均匀分布的电子束以相同的速度 从
从 的区间垂直于
的区间垂直于 点射入磁场的电子在磁场中的轨迹恰好经过
点射入磁场的电子在磁场中的轨迹恰好经过 点,忽略电子间的相互作用,不计电子的重力.
点,忽略电子间的相互作用,不计电子的重力.
 );
);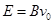 的匀强电场,在
的匀强电场,在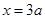 处垂直于
处垂直于 轴放置一平面荧光屏,与
轴放置一平面荧光屏,与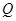 ,求:从O点上方最远处进入电场的粒子打在荧光屏上的位置。
,求:从O点上方最远处进入电场的粒子打在荧光屏上的位置。
 带电量为
带电量为 的带电粒子从电场中坐标为(-2L,-L)的点以速度v0沿+x方向射出,恰好经过原点O处射入区域Ⅰ又从M点射出区域Ⅰ(粒子的重力忽略不计)
的带电粒子从电场中坐标为(-2L,-L)的点以速度v0沿+x方向射出,恰好经过原点O处射入区域Ⅰ又从M点射出区域Ⅰ(粒子的重力忽略不计)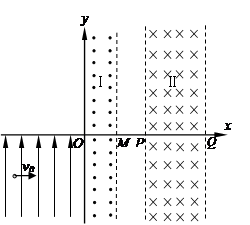


 ,板间距离为
,板间距离为 。当穿过线圈的磁通量增大且变化率为
。当穿过线圈的磁通量增大且变化率为 时,有一比荷为
时,有一比荷为 的带正电粒子以初速度
的带正电粒子以初速度 从上板的边缘射入板间,并恰好从下板的边缘射出;之后沿直线MN运动,又从N点射入另一垂直纸面向外磁感应强度为
从上板的边缘射入板间,并恰好从下板的边缘射出;之后沿直线MN运动,又从N点射入另一垂直纸面向外磁感应强度为 的圆形匀强磁场区(图中未画出),离开圆形磁场时速度方向偏转了
的圆形匀强磁场区(图中未画出),离开圆形磁场时速度方向偏转了 。不计带电粒子的重力。试求
。不计带电粒子的重力。试求
