题目内容
【题目】如图，轻绳OA一端系在天花板上，与竖直线夹角37°，轻绳OB水平，一端系在墙上，O点处挂一重为40N的物体．（cos37°=0.8，sin37°=0.6）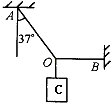
（1）求AO、BO的拉力各为多大？
（2）若AO、BO、CO所能承受的最大拉力均为100N，则所吊重物重力最大不能超过多大？
【答案】
（1）解：对结点O受力分析，如图所示：
根据共点力平衡条件，有：
TBO=Gtan37°=30N
答：OA、OB的拉力分别为50N、30N．
（2）解：O点受三个力作用而处于平衡状态，结合图中三角形知识，可知由于TOA＞TOC＞TOB，故：
G1=TOAcos37°=80N
答：所吊重物重力最大不能超过80N．
【解析】（1）对结点0受力分析，根据共点力平衡，运用合成法求出AO和BO绳子的拉力；（2）通过分析哪根绳子承受的拉力最大，从而求出重物的最大重力．
【考点精析】本题主要考查了力的分解的相关知识点，需要掌握求一个已知力的分力，叫做力的分解（力的分解与力的合成互为逆运算）；在实际问题中，通常将已知力按力产生的实际作用效果分解;为方便某些问题的研究，在很多问题中都采用正交分解法才能正确解答此题．
练习册系列答案
相关题目
