题目内容
9.如图甲所示,某均匀介质中各质点的平衡位置在同一条直线上,相邻两点间距离为d.质点1开始振动时速度方向竖直向上,振动由此开始向右传播.经过时间t,前13个质点第一次形成如图乙所示的波形.则该波的周期与波长分别为( )
| A. | $\frac{2}{3}t$ 9d | B. | $\frac{2}{3}t$ 8d | C. | $\frac{t}{2}$ $\frac{26}{3}d$ | D. | $\frac{t}{2}$ 8d |
分析 本题的关键是根据波传播的周期性和振动传播的特点,画出波的图象(振动应传播到第17个质点),或从第13个质点此时的振动方向向下数到再经$\frac{T}{2}$才能振动方向向上,从而找出周期T与时间t的关系,然后即可求解.
解答 解:根据振动的周期性和波的传播特点可知,质点13此时的振动方向向下,而波源的起振方向向上,所以从质点13算起,需要再经$\frac{T}{2}$振动的方向才能向上,即与波源的起振方向相同,设周期为T,则t=$\frac{3}{2}$T+$\frac{T}{2}$=2T,即T=$\frac{t}{2}$;
相邻波峰(或波谷)间的距离等于波长,由题意知波长为8d,故D正确.
故选:D
点评 “经过时间t,前13个质点第一次形成如图乙所示的波形”,并不说波只传到前13个质点.如果是只传到前13个质点,由于第13个质点此时振动方向向下,所以质点1开始运动时的速度方向也应该竖直向下,这与题给条件矛盾;熟记:任何质点的起振方向均与波源的起振方向相同.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.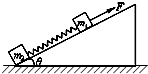 如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )
如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )
 如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )
如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的粗糙斜面上,物块与斜面间的动摩擦因数均为μ.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )| A. | 弹簧的弹力大小为$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$F | |
| B. | 弹簧的弹力大小为$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$F+μm2gcosθ | |
| C. | 地面对斜面的摩擦力一定水平向右 | |
| D. | 地面对斜面的摩擦力可能为零 |
1.一质点做简谐运动的图象如图所示,则下列说法正确的是 ( )


| A. | 质点振动的周期为0.4s | |
| B. | 0至0.5s内质点通过的路程为10cm | |
| C. | 在0.2s、0.4s时质点的振动速度相同 | |
| D. | 0.2s至0.3s内质点的加速度在增大,速度在减小. |
19.对下列现象解释正确的是( )


| A. | 图甲的原理和光导纤维传送光信号的原理一样 | |
| B. | 图乙的原理和音叉周围声音的强弱变化原理一样 | |
| C. | 图丙的原理和照相机镜头表面涂上增透膜的原理一样 | |
| D. | 图丁的原理和用标准平面检查光学平面的平整程度的原理一样 | |
| E. | 图戊的原理和门镜(透过门镜可以看到门外较宽阔的范围)的原理一样 |
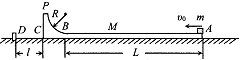 如图所示:质量M=0,6kg的滑板静止在光滑水平面上,其左端C距锁定装置D的水平距离l=0.5m,滑板的上表面由粗糙水平面和光滑$\frac{1}{4}$圆弧面在B点平滑对接而成,粗糙水平面长L=4m,圆弧的半径R=0.3m.现让一质量m=0.3kg,可视为质点的小滑块以大小vo=5m/s、方向水平向左的初速度滑上滑板的右端A.若滑板到达D处即被锁定,滑块返回B点时装置D即刻解锁,已知滑块与滑板间的动摩擦因数μ=0.2,重力加速度g=10m/s2.求:
如图所示:质量M=0,6kg的滑板静止在光滑水平面上,其左端C距锁定装置D的水平距离l=0.5m,滑板的上表面由粗糙水平面和光滑$\frac{1}{4}$圆弧面在B点平滑对接而成,粗糙水平面长L=4m,圆弧的半径R=0.3m.现让一质量m=0.3kg,可视为质点的小滑块以大小vo=5m/s、方向水平向左的初速度滑上滑板的右端A.若滑板到达D处即被锁定,滑块返回B点时装置D即刻解锁,已知滑块与滑板间的动摩擦因数μ=0.2,重力加速度g=10m/s2.求: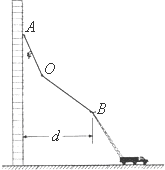 为了解决高楼救险中云梯高度不够高的问题,可在消防云梯上再伸出轻便的滑杆.被困人员使用安全带上的挂钩挂在滑杆上、沿滑杆下滑到消防云梯上逃生.通常滑杆由AO、OB两段直杆通过光滑转轴在O处连接,滑杆A端用挂钩钩在高楼的固定物上,且可绕固定物自由转动,B端用铰链固定在云梯上端,且可绕铰链自由转动,以便调节被困人员滑到云梯顶端的速度大小.设被困人员在调整好后的滑杆上下滑时滑杆与竖直方向的夹角保持不变,被困人员可看作质点、不计过O点时的机械能损失.已知AO长L1=6m、OB长L2=12m、竖直墙与云梯上端点B的水平距离d=13.2m,被困人员安全带上的挂钩与滑杆AO间、滑杆OB间的动摩擦因数均为μ=$\frac{5}{6}$.为了安全被困人员到达云梯顶端B点的速度不能超过6m/s,取g=10m/s2.
为了解决高楼救险中云梯高度不够高的问题,可在消防云梯上再伸出轻便的滑杆.被困人员使用安全带上的挂钩挂在滑杆上、沿滑杆下滑到消防云梯上逃生.通常滑杆由AO、OB两段直杆通过光滑转轴在O处连接,滑杆A端用挂钩钩在高楼的固定物上,且可绕固定物自由转动,B端用铰链固定在云梯上端,且可绕铰链自由转动,以便调节被困人员滑到云梯顶端的速度大小.设被困人员在调整好后的滑杆上下滑时滑杆与竖直方向的夹角保持不变,被困人员可看作质点、不计过O点时的机械能损失.已知AO长L1=6m、OB长L2=12m、竖直墙与云梯上端点B的水平距离d=13.2m,被困人员安全带上的挂钩与滑杆AO间、滑杆OB间的动摩擦因数均为μ=$\frac{5}{6}$.为了安全被困人员到达云梯顶端B点的速度不能超过6m/s,取g=10m/s2. 在大型货场,常通过传送带或斜面将不同的货物送上货车.这个过程简化为:质量不同的形状为正方体的货物一个一个地在斜面的顶端从静止沿斜面下滑,滑上放在水平地面上的长方体物块,货物从斜面滑上物块,速度大小不变,速度方向垂直于长方体物块左边缘,物块可能滑动,也可能仍然静止,货物可能静止在物块上,也可能滑出物块.斜面长s=2m,与水平面的夹角θ=30°,底端与物块上表面等高紧靠但不连接,如图所示.货物与斜面间动摩擦因数μ1=0.1,货物与物块间动摩擦因数μ2=0.4,物块长l=1.6m,质量m2=10kg,与地面间动摩擦因数μ3=0.2,货物质量用mi表示,5kg<m1<50kg.g取10m/s2,货物视为质点.求:
在大型货场,常通过传送带或斜面将不同的货物送上货车.这个过程简化为:质量不同的形状为正方体的货物一个一个地在斜面的顶端从静止沿斜面下滑,滑上放在水平地面上的长方体物块,货物从斜面滑上物块,速度大小不变,速度方向垂直于长方体物块左边缘,物块可能滑动,也可能仍然静止,货物可能静止在物块上,也可能滑出物块.斜面长s=2m,与水平面的夹角θ=30°,底端与物块上表面等高紧靠但不连接,如图所示.货物与斜面间动摩擦因数μ1=0.1,货物与物块间动摩擦因数μ2=0.4,物块长l=1.6m,质量m2=10kg,与地面间动摩擦因数μ3=0.2,货物质量用mi表示,5kg<m1<50kg.g取10m/s2,货物视为质点.求: