题目内容
4. 在大型货场,常通过传送带或斜面将不同的货物送上货车.这个过程简化为:质量不同的形状为正方体的货物一个一个地在斜面的顶端从静止沿斜面下滑,滑上放在水平地面上的长方体物块,货物从斜面滑上物块,速度大小不变,速度方向垂直于长方体物块左边缘,物块可能滑动,也可能仍然静止,货物可能静止在物块上,也可能滑出物块.斜面长s=2m,与水平面的夹角θ=30°,底端与物块上表面等高紧靠但不连接,如图所示.货物与斜面间动摩擦因数μ1=0.1,货物与物块间动摩擦因数μ2=0.4,物块长l=1.6m,质量m2=10kg,与地面间动摩擦因数μ3=0.2,货物质量用mi表示,5kg<m1<50kg.g取10m/s2,货物视为质点.求:
在大型货场,常通过传送带或斜面将不同的货物送上货车.这个过程简化为:质量不同的形状为正方体的货物一个一个地在斜面的顶端从静止沿斜面下滑,滑上放在水平地面上的长方体物块,货物从斜面滑上物块,速度大小不变,速度方向垂直于长方体物块左边缘,物块可能滑动,也可能仍然静止,货物可能静止在物块上,也可能滑出物块.斜面长s=2m,与水平面的夹角θ=30°,底端与物块上表面等高紧靠但不连接,如图所示.货物与斜面间动摩擦因数μ1=0.1,货物与物块间动摩擦因数μ2=0.4,物块长l=1.6m,质量m2=10kg,与地面间动摩擦因数μ3=0.2,货物质量用mi表示,5kg<m1<50kg.g取10m/s2,货物视为质点.求:(1)货物在斜面底端时的速度大小;
(2)货物滑上物块后,物块静止,货物的质量及在物块上表面滑动的最短距离;
(3)货物滑上物块后,物块滑动,恰好停在物块右边缘的货物的质量.
分析 (1)根据动能定理求的速度;
(2)货物滑上物块后,物块静货物收到摩擦力小于物块与地面的摩擦力,然后根据动能定理求的位移;
(3)根据牛顿第二定律和运动学公式求的质量即可.
解答 解:(1)设货物在斜面底端时的速度大小为v0,由动能定理,则${m_1}gssinθ-{μ_1}{m_1}gs=\frac{1}{2}{m_1}υ_0^2$
解得:v0=4m/s
(2)货物滑上物块后,物块静止,设货物质量为m11,则有μ2m11g≤μ3(m11+m2)g
解得:m11≤10kg
即质量小于等于10kg的货物滑上物块后,物块都静止.货物在物块上表面滑动的距离就是最短距离,设为x0,由动能定理得:$\frac{1}{2}{m_{11}}υ_0^2={μ_2}{m_{11}}g{x_0}$
代入数据解得:x0=2m
(3)货物滑上物块后,物块滑动,则货物质量大于10kg,设货物质量为m12,货物在物块上表面滑动的加速度为a1,物块加速度大小为a2,货物在物块表面滑动的时间为t,货物通过的距离为x1,物块通过的距离为x2,则μ2m12g=m12a1
m2a2=μ2m12g-μ3(m12+m2)g
υ0-a1t=a2t
${x_1}={υ_0}t-\frac{1}{2}{a_1}{t^2}$
${x_2}=\frac{1}{2}{a_2}{t^2}$
又:x1=x2+L
解得 a1=4m/s2,a2=1m/s2;m12=15kg
答:(1)货物在斜面底端时的速度大小是4m/s;
(2)货物滑上物块后,物块静止,货物的质量小于10kg;在物块上表面滑动的最短距离是2m;
(3)货物滑上物块后,物块滑动,恰好停在物块右边缘的货物的质量是15kg.
点评 本题考查动能定理及牛顿第二定律的应用,要注意明确研究对象,做好各过程的受力分析,明确物理规律的正确应用才能准确解题.


| A. | 该列波的波长为10cm | |
| B. | 若该列波沿x轴正向传播,则t=0时至t=0.2s时间内该列波至少传播了$\frac{2}{3}$个波长 | |
| C. | 若该列波沿x轴负向传播,则周期可能为0.15s | |
| D. | 若该列波的波速为1m/s,则该列波沿x轴负向传播 |
 如图所示,木块A、B静止叠放在光滑水平面上,A的质量为m,B的质量为2m.现施水平力F拉B(如图甲),A、B刚好不发生相对滑动,一起沿水平面运动.若改用水平力F′拉A(如图乙),使A、B也保持相对静止,一起沿水平面运动,则F′不得超过( )
如图所示,木块A、B静止叠放在光滑水平面上,A的质量为m,B的质量为2m.现施水平力F拉B(如图甲),A、B刚好不发生相对滑动,一起沿水平面运动.若改用水平力F′拉A(如图乙),使A、B也保持相对静止,一起沿水平面运动,则F′不得超过( )| A. | 2F | B. | $\frac{F}{2}$ | C. | 3F | D. | $\frac{F}{3}$ |

| A. | $\frac{2}{3}t$ 9d | B. | $\frac{2}{3}t$ 8d | C. | $\frac{t}{2}$ $\frac{26}{3}d$ | D. | $\frac{t}{2}$ 8d |
 如图所示,一个人站在水平地面上的长木板上用力F向右推箱子、木板、人、箱子均处于静止状态,三者的质量均为m,重力加速度为g.下列说法正确的是( )
如图所示,一个人站在水平地面上的长木板上用力F向右推箱子、木板、人、箱子均处于静止状态,三者的质量均为m,重力加速度为g.下列说法正确的是( )| A. | 箱子受到的摩擦力方向向右 | |
| B. | 人受到的摩擦力方向向右 | |
| C. | 地面对木板的摩擦力方向向右 | |
| D. | 若人用斜向下的力推箱子,则木板对地面的压力会大于3mg |

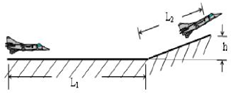 2012年11月23日上午,由来自东海舰队“海空雄鹰团”的飞行员戴明盟驾驶的中国航母舰载机歼-15降落在辽宁舰甲板上,首降成功,随后舰载机通过滑跃式起飞成功,滑跃式起飞有点像高山滑雪,主要靠甲板前端的上翘来帮助战斗机起飞,其示意图如图所示,设某航母起飞跑道主要由长度为L1=160m的水平跑道和长度为L2=20m的倾斜跑道两部分组成,水平跑道与倾斜跑道末端的高度差h=4.0m,一架质量为m=2.0×104kg的飞机,其喷气发动机的推力大小恒定为F=1.2×104N,方向与速度方向相同,在运动过程中飞机受到的平均阻力大小为飞机重力的0.1倍,假设航母处于静止状态,飞机质量视为不变并可看成质点,倾斜跑道看做斜面,不计拐角处的影响,取g=10m/s2
2012年11月23日上午,由来自东海舰队“海空雄鹰团”的飞行员戴明盟驾驶的中国航母舰载机歼-15降落在辽宁舰甲板上,首降成功,随后舰载机通过滑跃式起飞成功,滑跃式起飞有点像高山滑雪,主要靠甲板前端的上翘来帮助战斗机起飞,其示意图如图所示,设某航母起飞跑道主要由长度为L1=160m的水平跑道和长度为L2=20m的倾斜跑道两部分组成,水平跑道与倾斜跑道末端的高度差h=4.0m,一架质量为m=2.0×104kg的飞机,其喷气发动机的推力大小恒定为F=1.2×104N,方向与速度方向相同,在运动过程中飞机受到的平均阻力大小为飞机重力的0.1倍,假设航母处于静止状态,飞机质量视为不变并可看成质点,倾斜跑道看做斜面,不计拐角处的影响,取g=10m/s2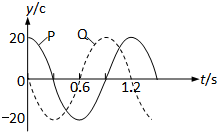 在一列横波的传播方向上有两点P和Q,两点间距离PQ=24m,它们的振动图象如图所示,P点距波源近.
在一列横波的传播方向上有两点P和Q,两点间距离PQ=24m,它们的振动图象如图所示,P点距波源近.