题目内容
15.在地球表面某高度处以一定的初速度水平抛出一个小球,测得水平射程为s,在另一星球表面以相同的水平速度抛出该小球,需将高度降低一半才可以获得相同的水平射程.忽略一切阻力.设地球表面重力加速度为g,该星球表面的重力加速度为g′,g:g′为( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | $\sqrt{2}$:1 | D. | 2:1 |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出时间,再根据水平初速度和时间求出位移,得出重力加速度的关系.
解答 解:根据h=$\frac{1}{2}$gt2得,t=$\sqrt{\frac{2h}{g}}$,则水平射程 s=v0t=v0$\sqrt{\frac{2h}{g}}$.
因为初速度相等,s相等,在星球上的高度变为地球上的一半,则重力加速度变为原来的一半,即 $\frac{g}{g′}$=2.故D正确,A、B、C错误.
故选:D
点评 解决本题的关键知道平抛运动的加速度为重力加速度,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
4.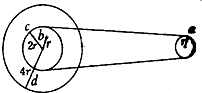 如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径是4r,小轮的半径是2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别为于小轮和大轮的边缘上,若在传动过程中皮带不打滑,则( )
如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径是4r,小轮的半径是2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别为于小轮和大轮的边缘上,若在传动过程中皮带不打滑,则( )
 如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径是4r,小轮的半径是2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别为于小轮和大轮的边缘上,若在传动过程中皮带不打滑,则( )
如图所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径是4r,小轮的半径是2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别为于小轮和大轮的边缘上,若在传动过程中皮带不打滑,则( )| A. | a点和b点的线速度大小相等 | B. | a点和b点的角速度大小相等 | ||
| C. | a点和c点的线速度大小相等 | D. | a点和d点的线速度大小相等 |
6.下列关于质点的说法中,正确的是( )
| A. | 质点是一个理想化的模型,实际并不存在,所以质点的建立在现实生活中没有什么意义 | |
| B. | 如果物体的形状和大小在所研究的问题中属于无关或次要因素,就可以把物体看作质点 | |
| C. | 凡是轻小的物体,都可看作质点 | |
| D. | 因为质点没有大小,所以与几何中心的点没有区别 |
7. 如图所示,虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( )
如图所示,虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( )
 如图所示,虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( )
如图所示,虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( )| A. | 带电粒子在Q点的加速度较大 | B. | 带电粒子在P点的加速度较大 | ||
| C. | 带电粒子在Q点的电场较强 | D. | 带电粒子在P点的电场较强 |
5.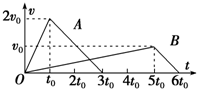 两个质点A、B放在同一水平面上,由静止开始从同一位置沿相同方向同时开始做直线运动,其运动的v-t图象如图所示.对A、B运动情况的分析,下列结论正确的是( )
两个质点A、B放在同一水平面上,由静止开始从同一位置沿相同方向同时开始做直线运动,其运动的v-t图象如图所示.对A、B运动情况的分析,下列结论正确的是( )
 两个质点A、B放在同一水平面上,由静止开始从同一位置沿相同方向同时开始做直线运动,其运动的v-t图象如图所示.对A、B运动情况的分析,下列结论正确的是( )
两个质点A、B放在同一水平面上,由静止开始从同一位置沿相同方向同时开始做直线运动,其运动的v-t图象如图所示.对A、B运动情况的分析,下列结论正确的是( )| A. | A、B加速时的加速度大小之比为2:1 | B. | 在t=6t0时刻,A、B相遇 | ||
| C. | 在t=3t0时刻,A、B相距最远 | D. | 在t=5t0时刻,A、B相距最远 |
 如图,实线为电场线,虚线为等势面且相邻两等势面的电势差相等,一正电荷在等势面φ3上时具有动能20J,它运动到等势面φ1上时,速度恰好为零,那么该电荷运动到等势面φ2时的动能为10J.令φ2=0,当该电荷的电势能为4J时,其动能大小为6J.
如图,实线为电场线,虚线为等势面且相邻两等势面的电势差相等,一正电荷在等势面φ3上时具有动能20J,它运动到等势面φ1上时,速度恰好为零,那么该电荷运动到等势面φ2时的动能为10J.令φ2=0,当该电荷的电势能为4J时,其动能大小为6J.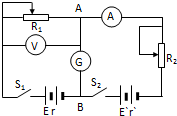 如图所示,可以通过辅助电源E′测量电源电动势E和内阻r.
如图所示,可以通过辅助电源E′测量电源电动势E和内阻r.