题目内容
20.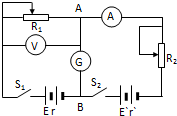 如图所示,可以通过辅助电源E′测量电源电动势E和内阻r.
如图所示,可以通过辅助电源E′测量电源电动势E和内阻r.(1)实验步骤是:①闭合开关S1、S2,调整R和R′使得灵敏电流表的示数为零,这时,A、B两点的电势φA、φB的关系是φA等于φB,即相当于同一点,读出电流表和电压表的示数I1和U1,其中I1就是通过电源E的电流.②改变滑动变阻器R1、R2的阻值,重新使得灵敏电流计示数为零,读出电流表和电压表的示数I2和U2.
(2)写出步骤①、②对应的电动势和内阻的表达式:
E=U1+$\frac{{I}_{1}({{U}_{2}-U}_{1})}{{{I}_{1}-I}_{2}}$,r=$\frac{{{U}_{2}-U}_{1}}{{{I}_{1}-I}_{2}}$.
(3)此方法从原理上没有(填“有”或“没有”)系统误差.
分析 本题是比较创新的实验,是属于研究性学习实验,是在常规实验基础上的改进,主要考查的是测量电源电动势和内阻、测金属电阻率的实验原理及误差的消除方法.本题都是两次测量,利用消元法消除了电表内阻造成的系统误差,提高了实验的准确度,根据闭合回路欧姆定律列出等式求解.
解答 解:(1)①闭合开关S1、S2,调节R和R′使得灵敏电流计G的示数为零,这时,A、B两点的电势φA、φB的关系是φA 等于φB,读出电流表和电压表的示数I1和U1,电流表测量的是干路上的电流,其中I1 等于通过电源E的电流.
②改变滑动变阻器R、R′的阻值,重新使得灵敏电流计示数为零.读出 电流表和电压表的示数I2和U2.
(2)根据闭合回路欧姆定律得
E=I1r+U1 E=I2r+U2
解得:E=U1+$\frac{{I}_{1}({{U}_{2}-U}_{1})}{{{I}_{1}-I}_{2}}$
r=$\frac{{{U}_{2}-U}_{1}}{{{I}_{1}-I}_{2}}$
(3)两次测量,调节R和R′使得灵敏电流计G的示数为零,使得AB之间的等效电阻为零,利用消元法消除了电表内阻造成的系统误差,所以E测 等于E真,r测 等于 r真 .此方法从原理上 没有系统误差
故答案为:(1)R和R′,等于;灵敏电流计示数为零,电流表和电压表的示数I2和U2
(2)U1+$\frac{{I}_{1}({{U}_{2}-U}_{1})}{{{I}_{1}-I}_{2}}$,$\frac{{{U}_{2}-U}_{1}}{{{I}_{1}-I}_{2}}$
(3)没有
点评 电学探究性实验有创新,要求考生对电学实验的基本知识很熟练而且能够灵活应用.是一道很好的题目,该题有一定难度.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
11.关于加速度,下列说法正确的是( )
| A. | 加速度是描述速度变化的物理量 | |
| B. | 速度的变化率就是加速度 | |
| C. | 加速度的方向总与速度的方向相同 | |
| D. | 加速度的方向总与速度变化量的方向相同 |
8. 甲乙两人同时同地出发骑自行车做直线运动,前1小时内的位移-时间图象如图所示.下列表述正确的是( )
甲乙两人同时同地出发骑自行车做直线运动,前1小时内的位移-时间图象如图所示.下列表述正确的是( )
 甲乙两人同时同地出发骑自行车做直线运动,前1小时内的位移-时间图象如图所示.下列表述正确的是( )
甲乙两人同时同地出发骑自行车做直线运动,前1小时内的位移-时间图象如图所示.下列表述正确的是( )| A. | 0.1-0.5小时内,甲的速度比乙的大 | |
| B. | 0.1-0.5小时内,甲的加速度比乙的大 | |
| C. | 0.6-0.8小时内,甲的位移比乙的小 | |
| D. | 0-0.8小时内,甲、乙的位移相等 |
15.在地球表面某高度处以一定的初速度水平抛出一个小球,测得水平射程为s,在另一星球表面以相同的水平速度抛出该小球,需将高度降低一半才可以获得相同的水平射程.忽略一切阻力.设地球表面重力加速度为g,该星球表面的重力加速度为g′,g:g′为( )
| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | $\sqrt{2}$:1 | D. | 2:1 |
12.初速度为v0的平抛物体,某时刻物体的水平分位移与竖直分位移大小相等,下列说法正确的是( )
| A. | 物体运动的时间为$\frac{2{v}_{0}}{g}$ | |
| B. | 该时刻物体的速率等于$\sqrt{5}$v0 | |
| C. | 该时刻物体的水平分速度与竖直分速度相等 | |
| D. | 该时刻物体位移大小等于$\frac{2\sqrt{2}{v}_{0}^{2}}{g}$ |
9. 雨滴下落中由于空气阻力作用而作匀速下降.汽车静止时,车内的人从矩形车窗ABCD看到窗外雨滴的运动方向如①所示.在汽车从静止开始匀加速启动阶段的t1、t2两个时刻,看到雨滴的运动方向分别如②、③所示.E是AB的中点.则( )
雨滴下落中由于空气阻力作用而作匀速下降.汽车静止时,车内的人从矩形车窗ABCD看到窗外雨滴的运动方向如①所示.在汽车从静止开始匀加速启动阶段的t1、t2两个时刻,看到雨滴的运动方向分别如②、③所示.E是AB的中点.则( )
 雨滴下落中由于空气阻力作用而作匀速下降.汽车静止时,车内的人从矩形车窗ABCD看到窗外雨滴的运动方向如①所示.在汽车从静止开始匀加速启动阶段的t1、t2两个时刻,看到雨滴的运动方向分别如②、③所示.E是AB的中点.则( )
雨滴下落中由于空气阻力作用而作匀速下降.汽车静止时,车内的人从矩形车窗ABCD看到窗外雨滴的运动方向如①所示.在汽车从静止开始匀加速启动阶段的t1、t2两个时刻,看到雨滴的运动方向分别如②、③所示.E是AB的中点.则( )| A. | t2=$\sqrt{2}$t1 | B. | t2=$\sqrt{3}$t1 | C. | t2=2t1 | D. | t2=3t1 |
10. 静电计是在验电器基础上制成,用其指针张角的大小来定性显示其金属球与外壳之间电势差大小.如图,A、B是平行板电容器的两个金属板,A板固定,手握B板的绝缘柄,G为静电计.开始时开关S闭合,静电计G指针张开一定角度.则( )
静电计是在验电器基础上制成,用其指针张角的大小来定性显示其金属球与外壳之间电势差大小.如图,A、B是平行板电容器的两个金属板,A板固定,手握B板的绝缘柄,G为静电计.开始时开关S闭合,静电计G指针张开一定角度.则( )
 静电计是在验电器基础上制成,用其指针张角的大小来定性显示其金属球与外壳之间电势差大小.如图,A、B是平行板电容器的两个金属板,A板固定,手握B板的绝缘柄,G为静电计.开始时开关S闭合,静电计G指针张开一定角度.则( )
静电计是在验电器基础上制成,用其指针张角的大小来定性显示其金属球与外壳之间电势差大小.如图,A、B是平行板电容器的两个金属板,A板固定,手握B板的绝缘柄,G为静电计.开始时开关S闭合,静电计G指针张开一定角度.则( )| A. | 保持S闭合,只将A、B两板靠近些,G指针张角变小 | |
| B. | 保持S闭合,只将A向上移动,G指针张角变大 | |
| C. | 断开S后,只将A、B两板分开些,G指针张角变小 | |
| D. | 断开S后,只在A、B两板间插入电介质,G指针张角变小 |
 矿井里的升降机从静止开始做匀加速直线运动,经过3s,它的速度达到3m/s;然后做匀速直线运动,经历6s后开始做匀减速运动,又经4.5m的距离后停止.求:
矿井里的升降机从静止开始做匀加速直线运动,经过3s,它的速度达到3m/s;然后做匀速直线运动,经历6s后开始做匀减速运动,又经4.5m的距离后停止.求: 如图所示,质量m=2.0×10-3kg的带电小球用绝缘轻细线竖直地悬于电场中,当小球带电量q1=1.0×10-4C时,悬线中的张力T1=1.5×10-2N,则小球所在处的场强多大?方向如何?当小球带电量q2=-1.0×10-4C时,悬线中的张力T2多大?(取g=10m/s2)
如图所示,质量m=2.0×10-3kg的带电小球用绝缘轻细线竖直地悬于电场中,当小球带电量q1=1.0×10-4C时,悬线中的张力T1=1.5×10-2N,则小球所在处的场强多大?方向如何?当小球带电量q2=-1.0×10-4C时,悬线中的张力T2多大?(取g=10m/s2)