题目内容
1. 一列横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.则:
一列横波如图所示,波长λ=8m,实线表示t1=0时刻的波形图,虚线表示t2=0.005s时刻的波形图.则:(1)波速多大?
(2)若2T>t2-t1>T,波速又为多大?
分析 (1)因为题中没有给出波的传播方向,故需要对波沿x轴正方向和x轴负方向传播分别进行讨论.又因为题中没有给出△t=t2-t1与周期T的关系,故需要考虑到波的重复性.运用波形平移法得出波的传播距离s与波长的关系,由v=$\frac{s}{t}$求得波速.
(2)波的一个周期内传播的距离是λ,当2T>t2-t1>T时,可知2λ>s>λ,根据上题结果分析求解本题.
解答 解:(1)若波沿x轴正方向传播,则可看出是波形传播的最小距离△x0=$\frac{1}{4}$λ=2m
波传播的可能距离是△x=△x0+nλ=8n+2(m)(n=0,1,2,3…)
则可能的波速为 v=$\frac{△x}{△t}$=$\frac{8n+2}{0.005}$=1600n+400(m/s),(n=0、1、2、…)
若波沿x轴负方向传播,则可看出是波形传播的最小距离△x0′=$\frac{3}{4}λ$=6m
波传播的可能距离是△x=△x0′+nλ=8n+6(m)
则可能的波速为 v=$\frac{△x}{△t}$=1600n+1200(m/s),(n=0、1、2…)
(2)当2T>t2-t1>T时,根据波动与振动的对应性可知2λ>△x>λ,这时波速的通解表达式中n=1.
若波沿x轴正方向传播,则波速为 v=1600n+400=2000(m/s)
若波沿x轴负方向传播,则波速为 v=1600n+1200=2800(m/s)
答:(1)若波沿x轴正方向传播,波速是1600n+400(m/s),(n=0、1、2、…);若波沿x轴负方向传播,波速是1600n+1200(m/s),(n=0、1、2…).
(2)若2T>t2-t1>T,若波沿x轴正方向传播,波速为2000(m/s);若波沿x轴负方向传播,波速为2800(m/s).
点评 本题关键抓住波的周期性和双向性,运用波形的平移法进行分析和求解,是典型的多解问题,不能漏解.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案| A. | 电子绕核运动有加速度,就要向外辐射电磁波 | |
| B. | 处于定态的原子,其电子做变速运动,但它并不向外辐射能量 | |
| C. | 原子内电子的可能轨道是不连续的 | |
| D. | 原、子能级跃迁时,辐射或吸收光子的能量取决于两个轨道的能量差 |
| A. | 一定质量的理想气体,体积减小时,单位体积的分子数增多,气体的压强一定增大 | |
| B. | 压缩处于绝热容器中的一定质量的理想气体,其内能一定增加 | |
| C. | 已知阿伏加德罗常数、某种气体的摩尔质量和密度,可以估算该种气体分子体积的大小 | |
| D. | 分子a从远处靠近不动的分子b的过程中,当它们相互作用力为零时,分子a的动能一定最大 |
 如图所示,小球的质量为m,自光滑的斜槽的顶端无初速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的动能和重力势能分别是(选取斜槽末端切线所在平面为参考平面)( )
如图所示,小球的质量为m,自光滑的斜槽的顶端无初速滑下,沿虚线轨迹落地,不计空气阻力,则小球着地瞬间的动能和重力势能分别是(选取斜槽末端切线所在平面为参考平面)( )| A. | mg(h+H),mgh | B. | mg(h+H),-mgh | C. | mgH,0 | D. | mgH,-mgH |
 汽车运动的速度-时间图象如图示,则汽车在2秒末的加速度是2m/s2,在8秒内的位移是33m.
汽车运动的速度-时间图象如图示,则汽车在2秒末的加速度是2m/s2,在8秒内的位移是33m.
 质量为m的圆形铜环,环面保持水平的从距桌H处无初速度向下运动,其正下方桌面上立着一条形磁铁,若环面刚要接触桌面的速度为v,则整个下落过程中铜环内产生的焦耳热量为mgH-$\frac{1}{2}$mV2.
质量为m的圆形铜环,环面保持水平的从距桌H处无初速度向下运动,其正下方桌面上立着一条形磁铁,若环面刚要接触桌面的速度为v,则整个下落过程中铜环内产生的焦耳热量为mgH-$\frac{1}{2}$mV2.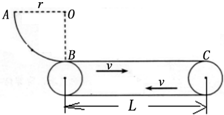 如图所示,固定的光滑$\frac{1}{4}$圆弧轨道AB的半径r=1.25m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.质量m=1kg的小物块(可视为质点)从轨道上的A点由静止释放,到达底端时水平进入轴心距离L=4m的水平传送带,传送带可由一电机驱使沿顺时针匀速转动.已知物体与传送带间的动摩擦因数为μ=0.15.不计物块通过轨道与传送带交接处的动能损失,不计空气阻力,(g=10m/s2)求:
如图所示,固定的光滑$\frac{1}{4}$圆弧轨道AB的半径r=1.25m,A点与圆心O在同一水平线上,圆弧轨道底端B点与圆心在同一竖直线上.质量m=1kg的小物块(可视为质点)从轨道上的A点由静止释放,到达底端时水平进入轴心距离L=4m的水平传送带,传送带可由一电机驱使沿顺时针匀速转动.已知物体与传送带间的动摩擦因数为μ=0.15.不计物块通过轨道与传送带交接处的动能损失,不计空气阻力,(g=10m/s2)求: