题目内容
【题目】如图所示，一物块分别沿倾角不等而底边相等的固定斜面1、2、3下滑，从静止开始由斜面顶端滑到底端．三个斜面的倾角分别是30°、45°、60°，不计物块与斜面间的摩擦，下列分析正确的是（ ）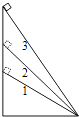
A.沿斜面3滑行时，物块的加速度最大
B.沿斜面2滑行时，物块的滑行时间最短
C.沿斜面2滑行时，物块到达斜面底端时的速度最大
D.沿斜面1、3滑行时，物块到达斜面底端时的速度一样大
【答案】A,B
【解析】解：A、设斜面倾角为θ，根据牛顿第二定律，有mgsinθ=ma，得a=gsinθ，θ越大，下滑的加速度越大，故A符合题意；
B、设斜面的底边长为L，则斜边长为 
，根据 
，得 
，解得：t= 
，当θ=45°时，时间最短，即物体沿斜面2滑行时，滑行的时间最短，故B符合题意；
CD、根据动能定理， 
，得 
，沿斜面3到达斜面底端的速度最大，故CD不符合题意；
所以答案是：AB
【考点精析】解答此题的关键在于理解匀变速直线运动的速度、位移、时间的关系的相关知识，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值．
练习册系列答案
阅读快车系列答案
相关题目
