题目内容
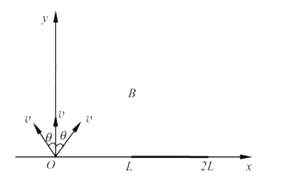
【题目】如图所示,x轴上方存在垂直纸面向外的匀强磁场,坐标原点处有一正离子源,单位时间在xOy平面内发射n0个速率为υ的离子,分布在y轴两侧各为θ的范围内。在x轴上放置长度为L的离子收集板,其右端点距坐标原点的距离为2L,当磁感应强度为B0时,沿y轴正方向入射的离子,恰好打在收集板的右端点。整个装置处于真空中,不计重力,不考虑离子间的碰撞,忽略离子间的相互作用。
(1)求离子的比荷![]() ;
;
(2)若发射的离子被收集板全部收集,求θ的最大值;
(3)假设离子到达x轴时沿x轴均匀分布。当θ=370,磁感应强度在B0 ≤B≤ 3B0的区间取不同值时,求单位时间内收集板收集到的离子数n与磁感应强度B之间的关系(不计离子在磁场中运动的时间)
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,有
时,有![]()
【解析】(1)洛伦兹力提供向心力,故![]() ,
,
圆周运动的半径R=L,解得![]()
(2)和y轴正方向夹角相同的向左和向右的两个粒子,达到x轴位置相同,当粒子恰好达到收集板最左端时,![]() 达到最大,轨迹如图1所示,
达到最大,轨迹如图1所示,
根据几何关系可知![]() ,解得
,解得![]()
(3)![]() ,全部收集到离子时的最小半径为R,如图2,有
,全部收集到离子时的最小半径为R,如图2,有![]() ,
,
解得![]()
当![]() 时,所有粒子均能打到收集板上,有
时,所有粒子均能打到收集板上,有![]()
![]() ,恰好收集不到粒子时的半径为
,恰好收集不到粒子时的半径为![]() ,有
,有![]() ,即
,即![]()
当![]() 时,设
时,设![]() ,解得
,解得![]()
当![]() 时,所有粒子都不能打到收集板上,
时,所有粒子都不能打到收集板上,![]()

练习册系列答案
相关题目