��Ŀ����
����Ŀ����ͼ��ʾ���ռ������ǿ��E =2.5��102N/C������ֱ���ϵ���ǿ�糡���ڵ糡��һ��ΪL=0.5m�ľ�Եϸ�ߣ�һ�˹̶���O�㣬һ��˩������m=0.5kg�������q=+4��10��2C��С��.�ֽ�ϸ����ֱ��ˮƽλ�ã�ʹС���ɾ�ֹ�ͷţ���С���˶���ߵ�ʱϸ���ܵ�������ǡ�ôﵽ���ܳ��ܵ����ֵ������.ȡg =10m/s2.��
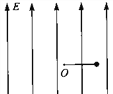
��1��ϸ���ܳ��ܵ����������
��2����С������˶�����O��ˮƽ�������ΪLʱ��С���O��ĸ߶�.
���𰸡���1��![]() m/s T=15N��2��
m/s T=15N��2��![]() =0.625m
=0.625m
��������������������ݶ��ܶ�����ʽ����ߵ���ٶȣ�����ߵ㣬�����ӵ������������͵糡���ĺ����ṩ��������ʽ��⣻���ӶϺ�С������ƽ���˶���
��1������ߵ㣬���ݶ��ܶ����ɵ�![]()
����ߵ㣬С��������������ӵ������������͵糡���ĺ����䵱������![]()
�������![]() m/s��T=15N
m/s��T=15N
��2��С������ƽ���˶���
��С����ˮƽ�����˶�L�Ĺ����У���ʱt������![]()
����ֱ�����ϣ����ٶ�Ϊ![]() ����
����![]()
�������![]() =0.625m
=0.625m

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ