题目内容

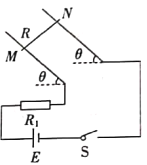
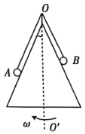
【题目】如图所示，A、B两小球用一根轻绳连接，轻绳跨过圆锥筒顶点处的光滑小定滑轮，圆锥筒的侧面光滑。当圆锥筒绕竖直对称轴OO′匀速转动时，两球都处于筒侧面上，且与筒保持相对静止，小球A到顶点O的距离大于小球B到顶点O的距离，则下列判断正确的是

A. A球的质量大

B. B球的质量大

C. A球对圆锥筒侧面的压力大

D. B球对圆锥筒侧面的压力大

【答案】BD

【解析】

绳对AB两球的拉力大小相等；分别对两球受力分析，根据正交分解法分别列出水平和竖直两个方向的方程即可进行讨论.

绳对AB两球的拉力大小相等，设绳子受到的拉力大小为T，侧面对小球的支持力大小为F，则Tcosθ+Fsinθ=mg，可知小球的质量m越大，F也就越大；又由Tsinθ-Fcosθ=mω2lsinθ，解得T=mgsinθ+ mω2lsinθcosθ；F=mgcosθ- mω2lsin2θ可知，质量m越大，F越大，l就越小，则B球的质量大，B球对圆锥筒侧面的压力越大，选项BD正确，AC错误；故选BD.

练习册系列答案
相关题目

【题目】嫦娥四号于2019年1月3日在月球背面着陆，嫦娥五号也讨划在今年发射。如果嫦娥五号经过若干次轨道调整后，先在距离月球表面h的高度处绕月球做匀速圆周运动，然后开启反冲发动机，嫦娥五号着陆器暂时处于悬停状态，最后实现软着陆，自动完成月面样品采集，并从月球起飞，返回地球。月球的半径为R且小于地球的半径，月球表面的重力加速度为g0且小于地球表面的重力加速度，引力常量为G。不考虑月球的自转，则下列说法正确的是

A. 嫦娥五号探测器绕月球做匀速圆周运动的速度可能大于地球的第一宇宙速度

B. 月球的平均密度

C. 嫦娥五号探测器在绕月球做匀速圆周运动的t时间内，绕月球运转圈数

D. 根据题目所给数据无法求出月球的第一宇宙速度

【题目】如图所示两平行倾斜导轨间的距离L=10cm，它们处于垂直导轨平面向下的磁场(图中未画出)中，导轨平面与水平方向的夹角θ=37°，在两导轨下端所接的电路中电源电动势E=10V内阻不计，定值电阻R1=4Ω，开关S闭合后，垂直导轨放置的质量m=10g、电阻R=6Ω的金属棒MN保持静止。已知金属棒MN与两导轨间的动摩擦因数μ=0.5，取sin37°=0.6，cos37°=08；g=10m/s2，认为最大静摩擦力等于滑动摩擦力。则磁场的磁感应强度大小可能是

A. 10T B. 1.5T C. 0.1T D. 1 T

【题目】如图所示，质量为M、长为L的木板置于光滑的水平面上，一质量为m的滑块放置在木板左端，滑块与木板间滑动摩擦力大小为f。现用一水平恒力F作用在滑块上，当滑块运动到木板右端时，木板在地面上移动的距离为s。下列说法正确的是（ ）

A. 其他条件不变的情况下，F增大，滑块与木板间产生的热量不变

B. 其他条件不变的情况下，M越大，s越大

C. 其他条件不变的情况下，F越大，滑块到达木板右端所用时间越长

D. 上述过程中，滑块克服摩擦力做功为f(L+s)

【题目】如图所示，质量相等、材料相同的两个小球A、B间用一劲度系数为k的轻质弹簧相连组成系统，系统穿过一粗糙的水平滑杆，在作用在B上的水平外力F的作用下由静止开始运动，一段时间后一起做匀加速运动，当它们的总动能为Ek时撤去外力F，最后停止运动．不计空气阻力，认为最大静摩擦力等于滑动摩擦力．则在从撤去外力F到停止运动的过程中，下列说法正确的是(　　)

A. 撤去外力F的瞬间，弹簧的伸长量为F/2k

B. 撤去外力F的瞬间，弹簧的伸长量为F/k

C. A克服外力所做的总功等于Ek/2

D. 系统克服摩擦力所做的功小于系统机械能的减少量

【题目】如图所示，一个匝数为n的圆形线圈，面积为S，电阻为r。将其两端a、b与阻值为R的电阻相连接，在线圈中存在垂直线圈平面向里的磁场区域，磁感应强度B随时间t均匀增加，当时线圈中产生的感应电流为I1；当时，其他条件不变，线圈中产生的感应电流变为I2。则通过电阻R的电流方向及I1与I2之比分别为

A. c→d，I1:I2=1:2

B. c→d，I1:I2=2:1

C. d→c，I1:I2=2:1

D. d→c，I1:I2=1:2

【题目】在“测金属丝的电阻率”实验中，提供以下实验器材：

待测金属丝、螺旋测微器(千分尺)、毫米刻度尺；电压表V(量程3 V，内阻约5 kΩ)、

电流表 A(量程0.6 A，内阻RA=1.0 Ω)；电源E(电动势约3 V)、滑动变阻器、开关及导线若干。

某同学进行了如下操作：

（1）用毫米刻度尺测金属丝的长度L；用螺旋测微器测金属丝直径d。

（2）按照实验设计的电路原理图（甲图）进行实物连接，请在乙图中连线_______。

（3）进行了相应测量，利用电压表和电流表的读数画出了如丙图所示的U－I图象，由此得到金属丝电阻R＝________ Ω。

（4）根据ρ＝________（用R、d、L及有关常数表示），即可计算该金属丝的电阻率。

【题目】两个带等量正电的点电荷，固定在图中P、Q两点，MN为PQ连线的中垂线，交PQ与O点，A为MN上的一点，一带负电的试探电荷q，从A点由静止释放，只在静电力作用下运动，取无限远处的电势为零，则（ ）

A. q由A向O的运动是匀加速直线运动 B. q由A向O运动的过程电势能逐渐减小

C. q运动到O点时的动能最大 D. q运动到O点时电势能为零

【题目】如图所示,正方形容器处在匀强磁场中,一束电子从孔A垂直于磁场射入容器中,其中一部分从C孔射出,一部分从D孔射出。下列叙述正确的是(　　)

A. 从C,D两孔射出的电子在容器中运动时的速度大小之比为1:2

B. 从C,D两孔射出的电子在容器中运动时间之比为1:2

C. 从C、D两孔射出的电子在容器中运动时的加速度大小之比为:1

D. 从C、D两孔射出的电子在容器中运动时的加速度大小之比为1:2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网