题目内容
17. 一质量M=0.8kg的小物块(可视为质点),用长l=0.8m的细绳悬挂在O点,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s 求:
一质量M=0.8kg的小物块(可视为质点),用长l=0.8m的细绳悬挂在O点,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s 求:(1)小球粘在物块上的瞬间,小球和物块共同速度的大小;
(2)小球和物块摆动过程中,细绳拉力的最大值;
(3)为使物块和小球能在竖直平面内做圆周运动,粘性小球的初速度不得小于多少?
分析 (1)因为小球与物块相互作用时间极短,所以小球和物块组成的系统动量守恒,根据动量守恒定律即可求解;
(2)小球和物块将以v开始运动时,轻绳受到的拉力最大,设最大拉力为F,根据向心力公式即可求解;
(3)由牛顿第二定律求出物块与小球恰好做圆周运动的速度,然后应用机械能守恒定律与动量守恒定律求出小球的速度.
解答 解:(1)因为小球与物块相互作用时间极短,小球和物块组成的系统动量守恒.以向右为正方向,由动量守恒定律得:
mv0=(M+m)v,
代入数据解得:v=2m/s;
(2)小球和物块将以v开始运动时,轻绳受到的拉力最大,设最大拉力为F,由牛顿第二定律得:
F-(M+m)g=(M+m)$\frac{{v}^{2}}{l}$,
代入数据解得:F=15N;
(3)物块与小球恰好做圆周运动,在最高点,重力提供向心力,由牛顿第二定律得:
(M+m)g=(M+m)$\frac{v{′}^{2}}{l}$,
代入数据解得:v′=2$\sqrt{2}$m/s,
从最低点到最高点过程,机械能守恒,由机械能守恒定律得:
$\frac{1}{2}$(M+m)v2=(M+m)gl+$\frac{1}{2}$(M+m)v′2,
小球击中物块过程系统动量守恒,以向右为正方向,由动量守恒定律得:
mv0=(M+m)v,
代入数据解得:v0=10$\sqrt{6}$m/s;
答:(1)小球粘在物块上的瞬间,小球和物块共同速度的大小为2m/s;
(2)小球和物块摆动过程中,细绳拉力的最大值为15N;
(3)为使物块和小球能在竖直平面内做圆周运动,粘性小球的初速度不得小于10$\sqrt{6}$m/s.
点评 本题主要考查了动量守恒定律、机械能守恒定律及向心力公式的直接应用,分析清楚物体运动过程是正确解题的关键,应用动量守恒定律、牛顿第二定律与机械能守恒定律可以解题,解题时注意物体做圆周运动临界条件的应用.

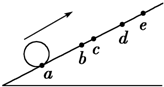 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,设小球经b、c时的速度分别为vb、vc,则( )| A. | vb=$\sqrt{8}$ m/s | B. | vc=3 m/s | ||
| C. | de=4 m | D. | 从d到e所用时间为2 s |
| A. | 布朗运动是分子的无规则运动 | |
| B. | 物体吸收了热量,温度升高,内能增大 | |
| C. | 物体温度越高,其分子平均动能越大 | |
| D. | 分子之间引力和斥力同时存在 |
| A. | P′A=7kg•m/s,p′B=9kg•m/s | B. | P′A=-3kg•m/s,p′B=19kg•m/s | ||
| C. | P′A=-6kg•m/s,p′B=22kg•m/s | D. | P′A=6kg•m/s,p′B=10kg•m/s |
| A. | 质点是一定是体积和质量都很小的物体 | |
| B. | 在研究行驶中汽车车轮的运动时可以把车轮看作质点 | |
| C. | 研究地球的公转时,地球不可以看做质点 | |
| D. | 质点是对物体的科学抽象,是一种理想的物理模型 |

| A. | 受重力、支持力和摩擦力 | B. | 受重力、支持力、向心力和静摩擦力 | ||
| C. | 重力和支持力 | D. | 支持力和向心力 |
 如图所示,有一水平传送带匀速向左运动,某时刻将一质量为m的小煤块(可视为质点)放到长为L的传送带的中点.它与传送带间的动摩擦因数为u:
如图所示,有一水平传送带匀速向左运动,某时刻将一质量为m的小煤块(可视为质点)放到长为L的传送带的中点.它与传送带间的动摩擦因数为u: