题目内容
7.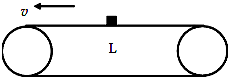 如图所示,有一水平传送带匀速向左运动,某时刻将一质量为m的小煤块(可视为质点)放到长为L的传送带的中点.它与传送带间的动摩擦因数为u:
如图所示,有一水平传送带匀速向左运动,某时刻将一质量为m的小煤块(可视为质点)放到长为L的传送带的中点.它与传送带间的动摩擦因数为u:(1)求小煤块刚开始运动时受到的摩擦力的大小和方向;
(2)若小煤块留在传送带上的印记长度恰好为$\frac{L}{2}$,求传送带的速度V.
分析 (1)根据小煤块与传送带之间的相对运动方向确定滑动摩擦力的方向,结合滑动摩擦力公式求出摩擦力的大小.
(2)小煤块速度与传送带速度相等后,一起做匀速直线运动,结合传送带位移与小煤块位移之差等于$\frac{L}{2}$,结合运动学公式求出传送带速度满足的条件
解答 解:(1)小煤块受到的摩擦力的大小f=μmg,方向水平向左. ①
(2)依题由牛顿第二定律,小煤块的加速度为:a=$\frac{F}{m}$=$\frac{μmg}{m}$=μg ②
设小煤块刚滑到纸带左端时速度正好与传送带速度相等,大小为v
由v=at,得:t=$\frac{v}{μg}$ ③
小煤块位移为:s1=$\frac{1}{2}$at2 ④
将②、③代入④得:s1=$\frac{1}{2}$μg•$\frac{{v}^{2}}{(μg)^{2}}$ ⑤
传送带位移为:s2=vt ⑥
由空间关系得:s2-s1=$\frac{L}{2}$ ⑦
将⑤、⑥代入 ⑦得:vt-$\frac{{v}^{2}}{2μg}$=$\frac{L}{2}$
解得:v=$\sqrt{μgL}$ ⑧
答:(1)小煤块刚开始运动时受到的摩擦力的大小为μmg,方向水平向左.
(2)传送带的速度v应满足的条件v=$\sqrt{μgL}$
点评 解决本题的关键知道小煤块在传送带上先做匀加速直线运动,当速度达到传送带速度后一起做匀速直线运动,结合牛顿第二定律和运动学公式灵活求解

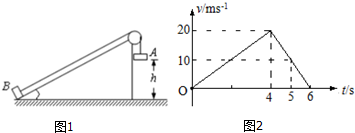
| A. | mgH-mgh-W | B. | W+mgH-mgh | C. | mgh+mgH-W | D. | W+mgh-mgH |
| A. | 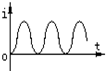 | B. |  | C. | 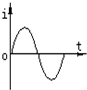 | D. | 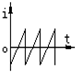 |
| A. | 飘落中的秋叶 | B. | 被掷出后在空中运动的铅球 | ||
| C. | 乘电梯匀速上升的人 | D. | 沿粗糙斜面匀速下滑的木箱 |
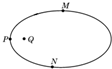 如图所示,带正电的点电荷Q固定,电子仅在库仑力作用下,做以Q为焦点的椭圆运动.M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.电子在从M经P到N点的过程中( )
如图所示,带正电的点电荷Q固定,电子仅在库仑力作用下,做以Q为焦点的椭圆运动.M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.电子在从M经P到N点的过程中( )| A. | 速度先减小后增大 | B. | M点的场强值大于N点场强 | ||
| C. | 电子在P点的加速度最大 | D. | 电子所受的电场力一直增大 |
| A. | 如果入射小球每次都从同一位置由静止滚下,重复几次落点应该是重合的 | |
| B. | 由于偶然因素的存在,重复几次的落点不重合也是正常的,但是落点应比较集中 | |
| C. | 测量P点位置时,如果重复10次的落点分别是P1、P2、P3、…、P10,则OP应是OP1、OP2、OP3、…、OP10的平均值 | |
| D. | 用半径尽量小的圆把P1、P2、P3、…、P10圈住,圆心就是落点平均位置P |
 一质量M=0.8kg的小物块(可视为质点),用长l=0.8m的细绳悬挂在O点,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s 求:
一质量M=0.8kg的小物块(可视为质点),用长l=0.8m的细绳悬挂在O点,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s 求: