题目内容
7.据报道,一儿童玩耍时不慎从45m高的阳台上无初速度掉下,在他刚掉下时恰被楼下一社区管理人员发现,该人员迅速由静止冲向儿童下落处的正下方楼底,准备接住儿童.已知管理人员到楼底的距离为18m,为确保能稳妥安全接住儿童,管理人员将尽力节约时间,但又必须保证接住儿童时没有水平方向的冲击.不计空气阻力,将儿童和管理人员都看作质点,设管理人员奔跑过程中只做匀速或匀变速运动,g取10m/s2.(1)管理人员至少用多大的平均速度跑到楼底?
(2)若管理人员在奔跑过程中做匀加速或匀减速运动的加速度大小相等,且最大速度不超过9m/s,求管理人员奔跑时加速度的大小需满足什么条件?
分析 (1)根据位移时间公式求出儿童自由落体运动的时间,结合位移和时间求出管理人员的最小平均速度.
(2)根据运动学公式判断出管理人员先加速、后匀速、再减速过程,抓住总位移和总时间,结合运动学公式求出管理人员奔跑时的加速度大小.
解答 解:(1)儿童下落过程,由运动学公式得,$h=\frac{1}{2}g{{t}_{0}}^{2}$ ①
管理人员奔跑的时间t≤t0 ②
对管理人员奔跑过程,由运动学公式得$s=\overline{v}t$ ③
由①②③联立并代入数据得,$\overline{v}$≥6 m/s.
(2)假设管理人员先匀加速接着匀减速奔跑到楼底,奔跑过程中的最大速度为v0,
由运动学公式得,$\overline{v}=\frac{0+{v}_{0}}{2}$,得${v}_{0}=2\overline{v}=12m/s>{v}_{max}$=9 m/s,再匀速,最后匀减速奔跑到楼底.
设匀加速、匀速、匀减速过程的时间分别为名;t1、t2、t3,位移分别为s1、s2、s3,
由运动学公式得,${s}_{1}=\frac{1}{2}a{{t}_{1}}^{2}$ ④,${s}_{3}=\frac{1}{2}a{{t}_{3}}^{2}$ ⑤,s2=vmaxt2 ⑥,
vmax=at1=at3 ⑦,
t1+t2+t3≤t0 ⑧,
s1+s2+s3=s ⑨
由④~⑨联立并代入数据得,a≥9 m/s2.
答:(1)管理人员至少用6m/s的平均速度跑到楼底;
(2)管理人员奔跑时加速度的大小需满足a≥9 m/s2.
点评 解决本题的关键理清管理人员在整个过程中的运动规律,抓住总时间和总位移,结合运动学规律灵活求解,难度中等.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
15. 木块A和B置于水平面上,它们的质量分别为ma和mb,与水平面的动摩擦因素都为μ.如图所示当水平力F作用于左端A上,两个物体一起加速运动时,AB间的作用力大小为N1.当同样大小的力F水平作用于右端B上,两物体一起加速运动时,AB间作用力大小为N2,则( )
木块A和B置于水平面上,它们的质量分别为ma和mb,与水平面的动摩擦因素都为μ.如图所示当水平力F作用于左端A上,两个物体一起加速运动时,AB间的作用力大小为N1.当同样大小的力F水平作用于右端B上,两物体一起加速运动时,AB间作用力大小为N2,则( )
 木块A和B置于水平面上,它们的质量分别为ma和mb,与水平面的动摩擦因素都为μ.如图所示当水平力F作用于左端A上,两个物体一起加速运动时,AB间的作用力大小为N1.当同样大小的力F水平作用于右端B上,两物体一起加速运动时,AB间作用力大小为N2,则( )
木块A和B置于水平面上,它们的质量分别为ma和mb,与水平面的动摩擦因素都为μ.如图所示当水平力F作用于左端A上,两个物体一起加速运动时,AB间的作用力大小为N1.当同样大小的力F水平作用于右端B上,两物体一起加速运动时,AB间作用力大小为N2,则( )| A. | N1+N2>F | B. | N1+N2<F | C. | N1+N2=F | D. | N1:N2=ma:mb |
2.A、B两个物体从同一地点开始在同一直线上做匀变速运动,它们的速度-时间图象如图所示,则( )
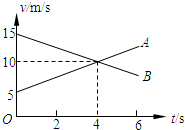

| A. | A、B两个物体的运动方向相反 | B. | t=4s时,两物体相遇 | ||
| C. | t=4s时,两物体距离最小 | D. | 相遇前,两物体最大距离为20m |
 一质量M=0.8kg的小物块(可视为质点),用长l=0.8m的细绳悬挂在O点,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s 求:
一质量M=0.8kg的小物块(可视为质点),用长l=0.8m的细绳悬挂在O点,处于静止状态.一质量m=0.2kg的粘性小球以速度v0=10m/s水平射向物块,并与物块粘在一起,小球与物块相互作用时间极短可以忽略,不计空气阻力,重力加速度g取10m/s 求: 从高度y=20m处以某一初速度水平抛出一物体,落到水平地面时的水平位移为x=6m,(g取10m/s2,不考虑空气助力)求:
从高度y=20m处以某一初速度水平抛出一物体,落到水平地面时的水平位移为x=6m,(g取10m/s2,不考虑空气助力)求: 图中画的是示波管的示意图,要使屏上的光点P向下偏移的距离增大,可采用的办法是( )
图中画的是示波管的示意图,要使屏上的光点P向下偏移的距离增大,可采用的办法是( ) 如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为Ep,现由静止释放A、B,B物块着地后速度立即变为0,同时弹簧锁定解除,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求:
如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接.第一次只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为Ep,现由静止释放A、B,B物块着地后速度立即变为0,同时弹簧锁定解除,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求: