Question

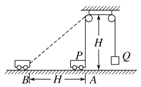
【题目】如图所示，一段绳子跨过距地面高度为H的两个定滑轮，一端连接小车P，另一端连接物块Q，小车最初在左边滑轮的正下方A点，以速度v从A点沿水平面匀速向左运动，运动了距离H到达B点（绳子足够长），下列说法中正确的有（　　）

A. 物块匀速上升

B. 物块在上升过程中处于超重状态

C. 车过B点时，物块的速度为

D. 车过B点时，左边绳子绕定滑轮转动的角速度为

Answer 1

【答案】BCD

【解析】

将小车的运动分解为沿绳子方向的运动，以及垂直绳子方向运动即绕滑轮的转动，根据沿绳子方向的运动速度和平行四边形定则求解物体的速度，再结合相应的公式求解。

A.将小车的运动分解为沿绳子方向的运动以及垂直绳子方向的运动，如图：

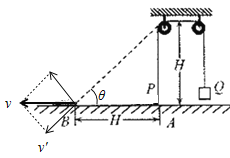
设此时绳子与水平方向增加的夹角为θ，则：tanθ＝H/H＝1，所以：θ＝45°；由三角函数可解得：当物体运动到绳与水平方向夹角为θ时物体的速度为v，则vcosθ＝v′，可知物体的运动不是匀加运动。故A错误；

B.由于vcosθ＝v′，随θ的减小，v′增大，所以物体向上做加速运动；加速度的方向向上，所以物体处于超重状态。故B正确；

C.当物体运动到B点，绳与水平方向夹角θ＝45°时物体的速度为v，则vcos45°＝v′，则v′＝v，故C正确；

D.物体运动到绳与水平方向夹角α＝45°时，左侧的绳子的长度是H，由图可知垂直于绳子方向的分速度为：v⊥＝vsin45°＝v，所以左边绳子绕定滑轮转动的角速度为： ．故D正确；

故选BCD。