Question

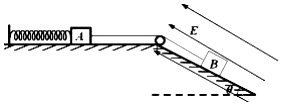
【题目】如图所示，为传送带传输装置示意图的一部分，传送带与水平地面的夹角θ＝37°，A、B两端相距L＝5.0 m，质量为M＝10 kg的物体以v0＝6.0 m/s的速度沿AB方向从A端滑上传送带，物体与传送带间的动摩擦因数处处相同，均为μ＝0.5。传送带顺时针运转的速度v (g取10 m/s2，sin 37°＝0.6，cos 37°＝0.8)。求：

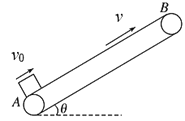
(1)若传送带速度v＝6.0 m/s，物体从A点到达B点所需的时间；

(2)若传送带速度v＝4.0 m/s，物体从A点到达B点的时间又是多少？

Answer 1

【答案】(1) t＝1s (2)t＝2.2s

【解析】（1）若传送带速度v＝6.0 m/s时μ<tanθ

物体的加速度沿斜面向下，其大小Mgsin θ-μMgcos θ＝Ma1

a1=2m/s2

L＝v0t-a2t2 t＝1 s(t＝5 s舍去)

（2）若传送带速度v＝4.0 m/s时

设物体速度大于传送带速度时加速度大小为a2，由牛顿第二定律得

Mgsin θ＋μMgcos θ＝Ma2

设经过时间t物体的速度与传送带速度相同，

通过的位移

设物体速度小于传送带速度时物体的加速度为a2

Mgsin θ－μMgcos θ＝Ma2

物体继续减速，设经t2速度到达传送带B点

L－x1＝vt2－a2t

联立可得：t＝t1＋t2＝2.2 s