题目内容
(18分)如图所示,劲度系数k=100N/m的一根轻质弹簧,右端固定在竖直墙壁上,左端连接一质量m=1.0kg的小物块,开始时弹簧处于原长,小物块静止于O点,现将小物块缓慢向左拉动至A点后释放,让小物块沿水平面向右运动起来,已知OA长度L=0.25m,小物块与水平面间的动摩擦因数μ=0.1,最大静摩擦力可看成等于滑动摩擦力的大小,g取10m/s2。
⑴试在坐标纸中作出小物块在由O移动到A的过程中,弹簧弹力F随伸长量x变化的F-x图象,类比于由v-t图象求位移的方法,求此过程中克服弹簧弹力做的功W;
⑵求小物块从A点向右运动过程中的最大速度v;
⑶求小物块从A点开始运动后,第一次到达最右端时,弹簧的形变量;
⑷求小物块从A点开始运动直至静止的总路程。
⑴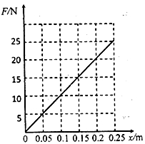 ,W=3.125J;
,W=3.125J;
⑵v=2.4m/s;⑶x1=0.23m;⑷s=3.12m
解析试题分析:根据胡克定律可知,弹簧弹力F与伸长量x的关系为:F=kx=100x,其中0≤x≤0.25m
其F-x图象如下图所示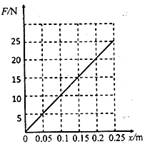
在F-x图象中图线与x轴所围的面积即表示了此过程中克服弹簧弹力做的功,有:W=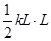 =3.125J
=3.125J
⑵小物块从A点向右运动过程中受重力mg、地面的支持力N和滑动摩擦力f,以及弹簧弹力F作用,根据牛顿第二定律分析可知,此时小物块向右先做加速度逐渐减小的加速运动,当加速度减小为零时,其速度达到最大,设此时弹簧的拉伸量为x0,有:kx0=μmg
解得:x0=0.01m
此过程中弹簧弹力做的功为:W0=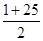 ×0.24J=3.12J
×0.24J=3.12J
根据动能定理有:W0-μmg(L-x0)=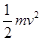 -0
-0
解得:v=2.4m/s
⑶设小物块第一次到达最右端时,弹簧的压缩量为x1,小物块从A点运动到最右端的过程中,弹簧弹力先做正功,后做负功,根据动能定理有: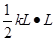 -
-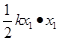 -μmg(L+x1)=0-0
-μmg(L+x1)=0-0
解得:L-x1=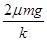 =0.02m,即x1=0.23m
=0.02m,即x1=0.23m
⑷设从A点释放小物块后,小物块共出现n次速度为零,且只要kx>μmg,小物块总能回到O点,在满足kx>μmg时,小物块每一次由最右端运动至最左端或由最左端运动至最右端(即小物块连续两次速度为零)的过程中,弹簧总是先做正功再做负功,设物块第n-1次速度为零时,弹簧的形变量为xn-1,第n次速度为零时,弹簧的形变量为xn,根据动能定理有: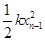 -
-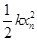 -μmg(xn-1+xn)=0-0
-μmg(xn-1+xn)=0-0
解得:Δx=xn-1-xn=0.02m
有:k(L-nΔx)≤μmg<k[L-(n-1)Δx],解得:12≤n<13,即取n=12
对全程,根据动能定理有: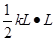 -
-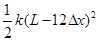 -μmgs=0-0
-μmgs=0-0
解得:s=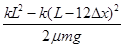 =3.12m
=3.12m
考点:本题主要考查了胡克定律、动能定理(功能关系)及图象的应用问题,属于较难题。

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案如图所示,物体质量为M,与弹簧A、B相连接,弹簧下端固定于地面上,弹簧A、B质量均不计,劲度系数分别为k1、k2。试求用手拉住弹簧A的上端,缓慢上移多大距离时能使弹簧B产生的弹力大小变成原来的2/3?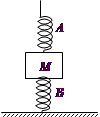
在水平桌面上有一个倾角为α的斜面体。一个质量为m的物块,在平行于斜面的拉力F作用下,沿斜面向上做匀速运动。斜面体始终处于静止状态。已知物块与斜面间的动摩擦因数为μ,重力加速度为g。下列结论正确的是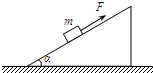
| A.斜面对物块的摩擦力大小是F | B.斜面对物块的摩擦力大小是μmgcosα |
| C.桌面对斜面体的摩擦力大小是0 | D.桌面对斜面体的摩擦力大小是Fcosα |
下列说法正确的是
| A.合力必大于分力 |
| B.运动物体所受摩擦力的方向一定和它运动方向相反 |
| C.物体受摩擦力时一定受弹力,而且这两个力的方向一定相互垂直 |
| D.处于完全失重状态下的物体不受重力作用 |
 B.L<
B.L< D.L>
D.L>
