题目内容
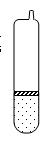
如图8-3-12所示,一连通器与贮水银的瓶M用软管相连,连通器的两支管竖直放置,粗细相同且上端封闭的均匀直管A和B内充有水银,水银面的高度差为h,水银面上方都是空气,气柱水均为2h,当气体的温度为T0(K)时,A管中气体的压强与3h高的水银产生的压强相等.现使气体的温度升高到1.5T0(K),同时调节M的高度,使B管中的水银面高度不变,问流入A管的水银柱的长度为多少?
图8-3-12
图8-3-12
0.15h
当温度为T0时,B管中气体的压强pb=pa+h=4h
当温度为1.5T0时,B管中气体体积不变,设其压强为p′B,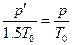
,解出p′=6h
设A管中水银面上升的高度为x,这时的压强为p′A
pA′=pB′-(h+x)=5h-x,这时A管中气柱长2h-x,由气态方程:
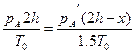得x2-7hx+h2=0,解得x=0.15h(另一根不合题意).
当温度为1.5T0时,B管中气体体积不变,设其压强为p′B,
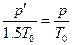,解出p′=6h设A管中水银面上升的高度为x,这时的压强为p′A
pA′=pB′-(h+x)=5h-x,这时A管中气柱长2h-x,由气态方程:
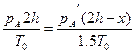得x2-7hx+h2=0,解得x=0.15h(另一根不合题意).
练习册系列答案
相关题目
，活塞静止时与气缸底部的距离为H，打开阀门K后，活塞下降．若将A、B内气体的温度都升高到
时，活塞仍可升高到原来的高度H．再让A、B内气体的温度恢复到
，并将活塞上的砝码取走，这时活塞又恢复到原来的高度H．若已知大气压强为
，活塞质量为m，活塞与气缸间摩擦可忽略不计．求容器B的容积
和活塞上砝码的质量m．
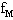=10N。气缸内壁光滑，横截面积S=2.5
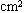。缸内有一个活塞封住一段空气柱。活塞质量m=2kg。开始时气柱长
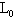=10cm。设g取10m／
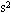，大气压p0取
Pa，气缸内气体温度保持不变，求
