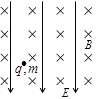题目内容
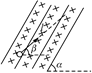
如图所示,AB和CD是足够长的平行光滑导轨,其间距为l,导轨平面与水平面的夹角为θ。整个装置处在磁感应强度为B、方向垂直于导轨平面向上的匀强磁场中,AC端连有电阻值为R的电阻。若将一质量M,垂直于导轨的金属棒EF在距BD端s处由静止释放,在EF棒滑至底端前会有加速和匀速两个运动阶段。今用大小为F、方向沿斜面向上的恒力把EF棒从BD位置由静止推至距BD端s处,突然撤去恒力F,棒EF先向上运动,最后又回到BD端。(金属棒、导轨的电阻均不计)求:

(1)EF棒下滑过程中的最大速度;
(2)请描述EF棒自撤去外力F又回到BD端整个过程的运动情况,并计算有多少电能转化成了内能?

(1)EF棒下滑过程中的最大速度;
(2)请描述EF棒自撤去外力F又回到BD端整个过程的运动情况,并计算有多少电能转化成了内能?
(1)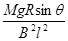 (2)Fs-
(2)Fs-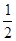 M(
M(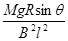 )2
)2
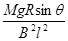 (2)Fs-
(2)Fs-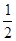 M(
M(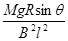 )2
)2 试题分析:(1)受力如图,安培力:F安=BIl=B
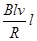
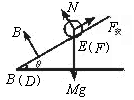
根据牛顿第二定律:a=
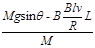
当a=0时速度达到最大值vm.有:Mgsinθ-B2l2vm/R="0"
得vm=
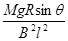
(2)棒先减速至零,然后从静止下滑,在滑回BD之前已达最大速度vm开始匀速
此过程中,设转化成的内能为ΔE. 根据能量守恒定律:Fs-ΔE=
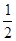 Mvm2 ③
Mvm2 ③ 得ΔE=Fs-
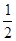 M(
M(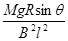 )2
)2 点评:本题考查了经典的传送带问题,要通过匀变速规律判断出相对运动的位移,通过能量守恒定律列式求解。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 =50cm。导轨处在垂直纸面向里的磁感应强度B=5T的匀强磁场中。一根电阻r=0.1Ω的金属棒ab可紧贴导轨左右运动。两块平行的、相距d=10cm、长度L=20cm的水平放置的金属板A和C分别与两平行导轨相连接,图中跨接在两导轨间的电阻R=0.4Ω,其余电阻忽略不计。已知当金属棒ab不动时,质量m=10g、带电量
=50cm。导轨处在垂直纸面向里的磁感应强度B=5T的匀强磁场中。一根电阻r=0.1Ω的金属棒ab可紧贴导轨左右运动。两块平行的、相距d=10cm、长度L=20cm的水平放置的金属板A和C分别与两平行导轨相连接,图中跨接在两导轨间的电阻R=0.4Ω,其余电阻忽略不计。已知当金属棒ab不动时,质量m=10g、带电量 的小球以某一速度
的小球以某一速度 沿金属板A和C的中线射入板间,恰能射出金属板(g取10m/s2)。求:
沿金属板A和C的中线射入板间,恰能射出金属板(g取10m/s2)。求:

 )从直角坐标系xOy平面内的坐标原点O以很小的速度进入匀强电场E1,计算时不计此速度且只考试xOy平面内的运动。求:
)从直角坐标系xOy平面内的坐标原点O以很小的速度进入匀强电场E1,计算时不计此速度且只考试xOy平面内的运动。求:
 ,半径为
,半径为 ,在与y轴成
,在与y轴成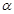 =
= 角的直径两端开有小孔
角的直径两端开有小孔 和
和 。现在桶内加匀强磁场,磁感应强度为
。现在桶内加匀强磁场,磁感应强度为 ,方向平行于轴线向外,该装置就是一个离子速度选择器。离子束以某一入射角从
,方向平行于轴线向外,该装置就是一个离子速度选择器。离子束以某一入射角从 的挡板,板上开有小孔
的挡板,板上开有小孔 (与
(与 时,探测器检测到有离子射入。不计离子重力和离子间的作用,打在桶壁和挡板上的离子不再反弹。试求:
时,探测器检测到有离子射入。不计离子重力和离子间的作用,打在桶壁和挡板上的离子不再反弹。试求: