��Ŀ����
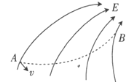
����Ŀ����һ�ڱڹ⻬�ľ�ԵϸԲ�����ɵ�Բ��BDC�̶�����ֱ���ڣ�Բ����Բ��ΪO��DΪԲ������͵㣬���С�BOC��![]() ��Բ���İ뾶ΪR��ˮƽ����BC���Ϸ�����ˮƽ���ҵķ�Χ�㹻�����ǿ�糡��Բ��O�����Ϸ�A����һ����Ϊm���������Ϊ��q��С����Ϊ�ʵ㣩����ֱ����С��Բ���ھ����ֽ���С�����ٶ��ͷţ�����һ��ʱ���С��պ�����ײ�ؽ���Բ���в�������Բ�����˶����������ٶ�Ϊg����
��Բ���İ뾶ΪR��ˮƽ����BC���Ϸ�����ˮƽ���ҵķ�Χ�㹻�����ǿ�糡��Բ��O�����Ϸ�A����һ����Ϊm���������Ϊ��q��С����Ϊ�ʵ㣩����ֱ����С��Բ���ھ����ֽ���С�����ٶ��ͷţ�����һ��ʱ���С��պ�����ײ�ؽ���Բ���в�������Բ�����˶����������ٶ�Ϊg����
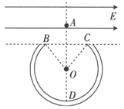
��1��A�㵽O��ľ��뼰��ǿ�糡�ĵ糡ǿ�ȴ�С��
��2��С���˶���Բ������͵�Dʱ��Բ������������
���𰸡���1��![]() ��2����3+
��2����3+![]() ��mg��������ֱ����
��mg��������ֱ����
��������
(1)С���ͷź��������͵糡�������������ȼ���ֱ���˶���С���B�������߷�����룬���ʱ�ٶȷ�������ֱ����ļн�Ϊ45���������ٶȷ�������ֱ����ļн�Ϊ45�������У�
![]()
��ã�
![]()
��Ϊ��BOC��![]() ��Բ���İ뾶ΪR����BC�ľ���Ϊ
��Բ���İ뾶ΪR����BC�ľ���Ϊ![]() ���ʸ��ݼ��ι�ϵ�п�֪��
���ʸ��ݼ��ι�ϵ�п�֪��
AO=![]()
(2)С���A�㵽D��Ĺ����У����ݶ��ܶ����ã�
![]()
��С���˶���Բ������͵�Dʱ������ţ�ٵڶ����ɵã�
![]()
������ã�
![]()
����ţ�ٵ������ɵ�С���˶���Բ������͵�Dʱ��Բ����ѹ����СΪ![]() ��������ֱ���¡�
��������ֱ���¡�
��(1)A�㵽O��ľ���![]() ,��ǿ�糡�ĵ糡ǿ�ȴ�С
,��ǿ�糡�ĵ糡ǿ�ȴ�С![]() ��
��
(2)С���˶���Բ������͵�Dʱ��Բ����������![]()

 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�