题目内容
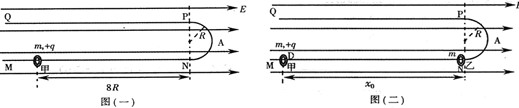
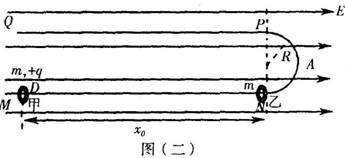
（21分）如图（一）所示的竖直平面内有范围足够大、水平向右的匀强电场，一轨道由两段直杆和一半径为0.20m的半圆环组成，固定在纸面所在的竖直平面内。直杆MN、PQ水平且足够长，MNAP段是光滑的（其中A点是半圆环的中点），PQ段是粗糙的。现有一质量为m、带电＋q的小环甲（可视为质点）套在MN杆上，它所受电场力为其重力的0.4倍。
（1）将小环甲从N点左侧1. 6m处由静止开始释放，如图（一），且知小环甲与直杆PQ间的动摩擦因数为0. 5，且最大静摩擦力与滑动摩擦力大小相等，求小环甲在水平杆PQ上通过的路程。
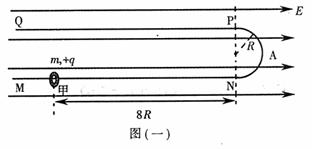
（2）若另一质量也为m、不带电的绝缘小环乙（视为质点）套在MN杆上的N点，如图（二），现从NM杆上的D点由静止释放小环甲，小环甲此后与乙碰撞时间极短，且碰后瞬间两者速度相同但不粘连，乙环沿NAP运动到P点时刚好停止，求DN间的距离x0。
解析：
（1）因为甲在PQ上运动s停下时，山子电场力小于摩擦力，将不再运动，对整个运动过程，由动能定理：
qE?L－mg?2R－qE?s－μmg?s＝0 4分
qE＝0.4mg 1分
得：s＝0.27m 3分
（2）甲、乙在N点碰撞前，设甲的速度为v，甲从D点到N点,由动能定理有：
qEx0＝
2分
设甲、乙在N点碰撞后的速度为vN ，由动量守恒守律有：
mv＝2m vN 2分
甲、乙整体从N点到A点，由动能定理有：
－mgR＋qER＝
－
3分
碰后甲乙共同运动到A点分离，由乙刚好能达到P点，从A到P，对乙由机械能守恒定律：mgR＝
3分
联立以上各式得：x0＝3.6m 3分
（2008?广州一模）如图（a）所示，竖直轻弹簧下端与放在水平地面上的物块A相连．上端与物块B相连．物块C在B的正上方某处自由落下，与B碰撞后粘合在一起．在物块C正上方放置一个速度传感器，以测量C下落的速度vC；在物块A的正下方放置一个压力传感器，以测量物块A对地面的压力N，得到如图（b）所示v-t和N-t图线，图中纵坐标轴上的P、v1、v2为已知量．已知弹簧的劲度系数为k，A、B、C三个物块的质量相等且都可视为质点，重力加速度为g，求：
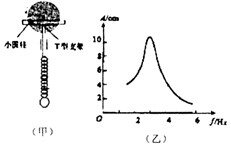如图（甲）所示，竖直圆盘转动时，可带动固定在圆盘上的T形支架在竖直方向振动，T形支架的下面系着一个弹簧和小球，共同组成一个振动系统．当圆盘静止时，小球可稳定振动．现使圆盘以4s的周期匀速转动，经过一段时间后，小球振动达到稳定．改变圆盘匀速转动的周期，其共振曲线（振幅A与驱动力的频率f的关系）如图（乙）所示，则（ ）| A、此振动系统的固有频率约为3Hz | B、此振动系统的固有频率约为0.25Hz | C、若圆盘匀速转动的周期增大，系统的振动频率不变 | D、若圆盘匀速转动的周期增大，共振曲线的峰值将向右移动 |
