题目内容
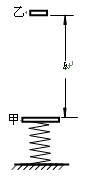
如图所示,一轻质弹簧竖直固定在地面上,上面连接一个质量m1=1.0kg的物体A,平衡时物体下表面距地面h1= 40cm,弹簧的弹性势能E0=0.50J。在距物体m1正上方高为h= 45cm处有一个质量m2=1.0kg的物体B自由下落后,与物体A碰撞并立即以相同的速度运动(两物体粘连在一起),当弹簧压缩量最大时,物体距地面的高度h2=6.55cm。g=10m/s2。

(1)已知弹簧的形变(拉伸或者压缩)量为x时的弹性势能 ,式中k为弹簧的劲度系数。求弹簧不受作用力时的自然长度l0;
,式中k为弹簧的劲度系数。求弹簧不受作用力时的自然长度l0;
(2)求两物体做简谐运动的振幅;
(3)求两物体运动到最高点时的弹性势能。

(1)已知弹簧的形变(拉伸或者压缩)量为x时的弹性势能
 ,式中k为弹簧的劲度系数。求弹簧不受作用力时的自然长度l0;
,式中k为弹簧的劲度系数。求弹簧不受作用力时的自然长度l0;(2)求两物体做简谐运动的振幅;
(3)求两物体运动到最高点时的弹性势能。
(1)0.50m (2)23.45cm (3)6.0×10-2J
(1)设物体A在弹簧上平衡时弹簧的压缩量为x1,弹簧的劲度系数为k
根据力的平衡条件有 m1g=k x1
而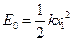
解得:k=100N/m, x1=0.10m
所以,弹簧不受作用力时的自然长度l0=h1+x1=0.50m
(2)两物体运动过程中,弹簧弹力等于两物体总重力时具有最大速度,此位置就是两物体粘合后做简谐运动的平衡位置
设在平衡位置弹簧的压缩量为x2,则 (m1+ m2)g=kx2,解得:x2=0.20m,
设此时弹簧的长度为l2,则 l2=l0-x2 ,解得:l2="0.30m" ,
当弹簧压缩量最大时,是两物体振动最大位移处,此时弹簧长度为h2=6.55cm
两物体做简谐运动的振幅A=l2-h2 =23.45cm
(3)设物体B自由下落与物体A相碰时的速度为v1,则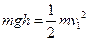
解得:v1=3.0m/s,
设A与B碰撞结束瞬间的速度为v2,根据动量守恒 m2 v1=(m1+ m2)v2,
解得:v2="1.5" m/s,
由简谐运动的对称性,两物体向上运动过程达到最高点时,速度为零,弹簧长度为l2+A=53.45cm
碰后两物体和弹簧组成的系统机械能守恒,设两物体运动到最高点时的弹性势能EP,则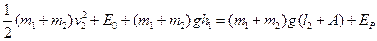
解得EP=6.0×10-2J。
根据力的平衡条件有 m1g=k x1
而
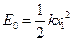
解得:k=100N/m, x1=0.10m
所以,弹簧不受作用力时的自然长度l0=h1+x1=0.50m
(2)两物体运动过程中,弹簧弹力等于两物体总重力时具有最大速度,此位置就是两物体粘合后做简谐运动的平衡位置
设在平衡位置弹簧的压缩量为x2,则 (m1+ m2)g=kx2,解得:x2=0.20m,
设此时弹簧的长度为l2,则 l2=l0-x2 ,解得:l2="0.30m" ,
当弹簧压缩量最大时,是两物体振动最大位移处,此时弹簧长度为h2=6.55cm
两物体做简谐运动的振幅A=l2-h2 =23.45cm
(3)设物体B自由下落与物体A相碰时的速度为v1,则
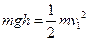
解得:v1=3.0m/s,
设A与B碰撞结束瞬间的速度为v2,根据动量守恒 m2 v1=(m1+ m2)v2,
解得:v2="1.5" m/s,
由简谐运动的对称性,两物体向上运动过程达到最高点时,速度为零,弹簧长度为l2+A=53.45cm
碰后两物体和弹簧组成的系统机械能守恒,设两物体运动到最高点时的弹性势能EP,则
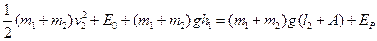
解得EP=6.0×10-2J。

练习册系列答案
相关题目

 B.
B.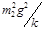
 D.
D.