Question

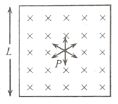
【题目】如图所示，在边长为L的正方形区域内有垂直纸面向里的匀强磁场，在区域中心处有一粒子源P，粒子源P沿平行纸面的各个方向均匀地射出大量的质量为m、电荷量为q、速度为v的相同粒子，不计粒子的重力及粒子间的作用力，问：

(1)若要使所有粒子都无法射出磁场区域，求区域内磁感应强度的最小值B0；

(2)若区域内匀强磁场的磁感应强度为B0，求该区域内没有粒子到达的地方的面积；

(3)若区域内磁感应强度，求能从边界逸出的粒子数与P点射出的总粒子数的比值k。

Answer 1

【答案】(1)；(2)；(3)

【解析】

(1)如图

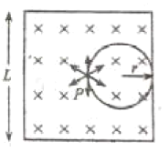
由几何关系知粒子运动的轨道半径

再由磁场中粒子运动规律

即

联立解得

故区域内磁感应强度的最小值

(2)如图

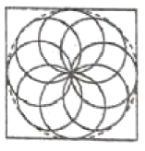
可知所有轨道的包络线（虚线）为半径为的圆，故粒子无法到达的地方的面积

(3)设此时粒子运动轨道半径为，把

代入，解得

能够从边界逸出的粒子轨道如图所示

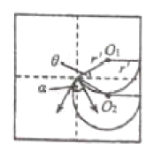
由图中几何关系得

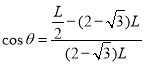
解得

两边界对应的速度夹角

故