��Ŀ����
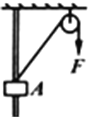
����Ŀ��һ�ᵯ�ɵ�һ�˹̶������Ϊ![]() �Ĺ̶��⻬б��ĵײ�����һ�˺�����Ϊ2m��С���A����������Ϊm��С���B����A��ֹ��б���ϣ���ͼ��ʾ����ʱ���ɵ�ѹ����Ϊx0����t=0ʱ��ʼ����Bʩ����б�����ϵ�������ʹBʼ�������ٶ�Ϊa���ȼ���ֱ���˶�������һ��ʱ������A��B���롣���ɵ��α�ʼ���ڵ������ڣ��������ٶȴ�СΪg����
�Ĺ̶��⻬б��ĵײ�����һ�˺�����Ϊ2m��С���A����������Ϊm��С���B����A��ֹ��б���ϣ���ͼ��ʾ����ʱ���ɵ�ѹ����Ϊx0����t=0ʱ��ʼ����Bʩ����б�����ϵ�������ʹBʼ�������ٶ�Ϊa���ȼ���ֱ���˶�������һ��ʱ������A��B���롣���ɵ��α�ʼ���ڵ������ڣ��������ٶȴ�СΪg����![]() ��m��x0��a����֪��������˵����ȷ������ ��
��m��x0��a����֪��������˵����ȷ������ ��
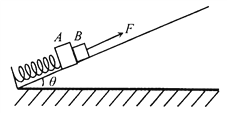
A. ������֪������������ӿ�ʼ�����A��B�������õ�ʱ��
B. ������֪��������������A��B����ʱ���ٶȴ�С
C. ���A��B����ʱ�����ɵĵ���ǡ��Ϊ��
D. ���A��B��������A��ʼ����
���𰸡�AB
��������A��B��AB��ֹʱ�� ![]() ,��
,��![]() ����Bʩ����б�����ϵ�������A��Bһ�����ȼ����˶�������ʱA��B�䵯��Ϊ�㣬���ٶȾ�Ϊa�����ʱ���ɱ�ѹ��x,���A�У�
����Bʩ����б�����ϵ�������A��Bһ�����ȼ����˶�������ʱA��B�䵯��Ϊ�㣬���ٶȾ�Ϊa�����ʱ���ɱ�ѹ��x,���A�У� ![]() ,��
,��![]() ��
�� ![]() �����������
����������� 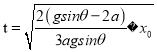 ,
, 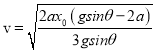 ��AB��ȷ��
��AB��ȷ��
C�����A��B����ʱ�����ɵĵ�����Ϊ�㣬A��B�䵯��Ϊ�㣬��ʱ���ɵ���![]() ��C����
��C����
D������ʱ��A�����ϵļ��ٶȣ�֮���������ٶȼ�С�ļ����˶����ﵽ����ٶȺ����������˶���D����
��ѡAB��

��ϰ��ϵ�д�
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�
�����Ŀ