题目内容
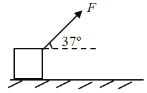
【题目】如图所示,一次训练中，运动员腰部系着不可伸长的绳拖着质量m=11 kg的轮胎从静止开始沿着笔直的跑道加速奔跑，绳与水平跑道的夹角是37°，5 s后拖绳从轮胎上脱落，轮胎运动的v-t图象如右图所示，不计空气阻力，已知sin 37°=0.6，cos 37°=0.8，g取10 m/s2，则下列说法正确的是（ ）
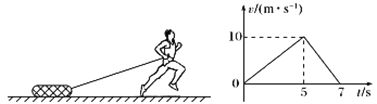
A. 在5～7s内轮胎与水平地面间的滑动摩擦力是55N
B. 在0～5s内轮胎与水平地面间的滑动摩擦力是55N
C. 在0～5s内，轮胎克服摩擦力做功为850 J
D. 在6 s末，摩擦力的瞬时功率大小为275 W
【答案】ACD
【解析】
根据速度时间图线得出匀减速直线运动的加速度和匀加速直线运动的加速度，结合牛顿第二定律求出动摩擦因数以及拉力的大小。根据速度时间公式求出6s末的速度，结合瞬时功率公式求出6s末拉力的瞬时功率。根据功的定义，求出轮胎克服摩擦力做功的大小。
5～7s的加速度为：
，根据牛顿第二定律：
，所以在5～7s内轮胎与水平地面间的滑动摩擦力是55N，故A正确；由上可知胎与水平地面间的动摩擦因数为：
，0～5s的加速度为：
，根据牛顿第二定律：Fcos37°-μ（mg-Fsin37°）=ma2，代入数据解得F=70N，在0～5s内轮胎与水平地面间的滑动摩擦力是：f2=μ（mg-Fsin37°）=34N，故B错误；在0～5s内的位移为：
，轮胎克服摩擦力做功为：
，故C正确；6s末的瞬时速度v=a1t=5m/s，故瞬时功率P=μmgv=275W，故D正确。所以ACD正确，B错误。
练习册系列答案
相关题目
