题目内容
【题目】如图,一玻璃工件的上半部是底面半径为R的圆锥体,O点为圆心,高为R;下半部是半径为 R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从圆锥曲面射入,该光线与OC之间的距离为0.5R。已知最后从圆锥曲面射出的光线恰好与入射光线平行(不考虑多次反射),求:
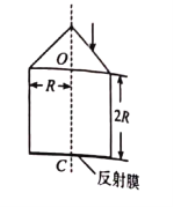
(i)从圆锥曲面射入的光线的入射角为多少:
(ii)若光在真空中的传播速度为c,试计算光在该玻璃工件内传播的时间。
【答案】(i)45°(ii)![]()
【解析】
根据光路的对你性和光路可逆性,与入时光线相对于OC轴对称的出射光线与入射光线平行。故从圆锥曲面射入的折射光线,将从圆柱体底面中心C点反射,光路图如图所示。

(i)由几何关系,得从圆锥曲面射入的光线的入射角为45°;
(ii)由折射定律,得
n=![]()
在△AOC中,由正弦定理,得
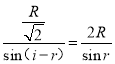
联立解得
n=![]()
由n=![]() 得光在该玻璃内传播的速度为
得光在该玻璃内传播的速度为
![]()
由几何关系得
AC=![]()
故光程为
s=2AC=![]() R
R
光在该玻璃工件内传播的时间为
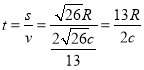

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目