题目内容
15.如图所示,质量m=0.015kg的木块Q放在水平桌面上的A点.A的左边光滑,右边粗糙,与木块间的动摩擦因数μ=0.08.在如图所示的矩形区域内存在竖直向上的匀强电场和水平向里的匀强磁场,磁感应强调B=1T.场区的水平宽度d=0.8m,竖直方向高h=0.6m.带正电的小球P,质量M=0.03kg,电荷量q=0.015C,以v0=0.5m/s的初速度向Q运动.与Q发生正碰后,P在电、磁场中做匀速圆周运动且运动的总时间t=4.0s.不计P和Q的大小,P、Q碰撞时无电量交换,重力加速度g取10m/s2,计算时取π=3,试求: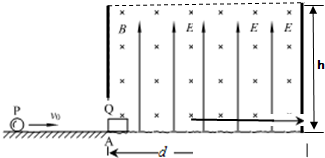
(1)匀强电场的电场强度E;
(2)P从电、磁场中出来时的速度大小和方向;
(3)如果P和Q碰撞时,系统满足Mv0+0=Mv+mQvQ(v为碰后P的速度,vQ为碰后Q的速度),求P从电、磁场中出来的时刻,Q所处的位置.
分析 (1)带电粒子在复合场中做圆周运动,一定满足电场力与重力平衡,洛仑兹力充当向心力;
(2)由洛仑兹力充当向心力,结合几何关系可求得最终的速度方向和大小;
(3)PQ碰撞过程动量守恒,由动量守恒定律可求得碰后的速度,再由牛顿第二定律可求得P离开时的位置.
解答  解:(1)P进入电、磁场后,受电场力、重力、洛伦兹力三力作用做匀速圆周运动
解:(1)P进入电、磁场后,受电场力、重力、洛伦兹力三力作用做匀速圆周运动
可见电场力与重力大小相等方向相反,两力平衡
相当于P在电、磁场中只受洛仑兹力作用,洛仑兹力等于向心力
所以电场力F=qE=G=mg=0.3N
解得:E=20 N/C
(2)P在磁场中受洛伦兹力提供P作圆周运动的向心力故有qvB=m$\frac{{v}^{2}}{R}$;
得P做圆周运动的半径R=$\frac{mv}{Bq}$;
周期T=$\frac{2πm}{Bq}$
代入数据得T=12s
由已知条件,有t=4.0s=$\frac{T}{12}$+$\frac{T}{4}$
故如下图所示:
P的轨迹圆心角θ=30°
由右图可知,轨迹半径R+Rsin30°=0.6m
所以R=0.4m
结合①式得v=0.2m/s;
方向:与磁场上边界夹角为60°
(3)P和Q碰撞时,有mv0=mv+mQvQ
代入数据可解得vQ=0.6m/s
碰撞后Q水平方向只受摩擦力作用,应用牛顿第二定律,有μmg=ma得
a=0.8m/s2
因为Q在摩擦力作用下做匀减速直线运动,取速度为正方向,故加速度a=-0.8m/s2
则Q停下前运动时间t′=$\frac{0-v}{a}$=$\frac{0-0.6}{-0.8}$=0.75s
由于t′<t=4s,说明P离开电、磁场时,Q已经停下
故位移x═$\frac{0-{v}^{2}}{2a}$=$\frac{0-0.{6}^{2}}{2×(-0.8)}$=0.225m
即Q停留在右方距初始位置0.225m处.
答:(1)通过受力分析判断碰后P球在电、磁场中做匀速圆周运动;
(2)P从电、磁场中出来时的速度v=0.2m/s;
(3)P从电、磁场中出来的时刻,Q停留在右方距初始位置0.225m处.
点评 本题综合考查动量守恒、带电粒子在复合场中的运动及牛顿第二定律等,关键在于正确分析题意及物理过程,将其分解为若干小的问题进行处理,同时注意掌握各过程之间的关系.

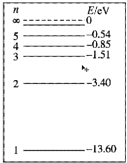 用大量具有12.5eV动能的电子,撞击大量处于基态的氢原子,观测到了一定数量的氢原子的光谱线.氢原子的能级图如图所示,下列说法中正确的是( )
用大量具有12.5eV动能的电子,撞击大量处于基态的氢原子,观测到了一定数量的氢原子的光谱线.氢原子的能级图如图所示,下列说法中正确的是( )| A. | 实验中能产生三种频率的谱线 | |
| B. | 波长最长的光子具有的能量为1.89eV | |
| C. | 频率最高的光子具有的能量为12.5eV | |
| D. | 电子撞击后的动能一定为2.3eV |
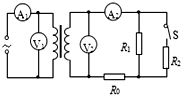 如图是通过理想变压器降压给用户供电的示意图.变压器输入电压是市区电网的电压,负载变化时输入电压不会有大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,开关S闭合后,相当于接入电路中工作的用电器增加.则关于开关S闭合后,以下说法正确的是( )
如图是通过理想变压器降压给用户供电的示意图.变压器输入电压是市区电网的电压,负载变化时输入电压不会有大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,开关S闭合后,相当于接入电路中工作的用电器增加.则关于开关S闭合后,以下说法正确的是( )| A. | 电表V1示数不变,V2示数减小 | B. | 电表A1示数增大、A2示数增大 | ||
| C. | 原线圈输入功率减小 | D. | 电阻R1两端的电压减小 |
| A. | “嫦娥三号”探月卫星匀速飞行的速度为$\frac{2πNR}{t}$ | |
| B. | 月球的平均密度为$\frac{3πM{N}^{2}}{g{r}^{2}{t}^{2}}$ | |
| C. | “嫦娥三号”探月卫星的质量为$\frac{4{π}^{2}{N}^{2}{r}^{3}}{g{R}^{2}{t}^{2}}$ | |
| D. | “嫦娥三号”探月卫星绕月球表面匀速飞行的向心加速度为$\frac{4{π}^{2}{N}^{2}r}{{t}^{2}}$ |
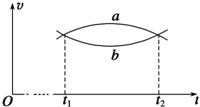 如图所示,两条曲线为汽车a、b在同一条平直公路上的v-t图象,已知在t2时刻,两车相遇,下列说法正确的是( )
如图所示,两条曲线为汽车a、b在同一条平直公路上的v-t图象,已知在t2时刻,两车相遇,下列说法正确的是( )| A. | 在t1~t2时间内,a车加速度先减小后增大 | |
| B. | 在t1~t2时间内,a车的位移比b车的小 | |
| C. | t2时刻可能是b车追上a车 | |
| D. | t1时刻前的某一时刻两车可能相遇 |
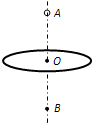 如图所示,一固定的水平玻璃圆环均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.现将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度υ0,重力加速度为g,则下列判断正确的是( )
如图所示,一固定的水平玻璃圆环均匀带上电荷,其中心O的正上方和正下方分别有两点A、B,OA=OB=h.现将一质量为m的带正电小球放在A点时恰好处于静止状态,若给小球一个沿竖直向下的初速度υ0,重力加速度为g,则下列判断正确的是( )| A. | 带电圆环在B点产生的场强方向竖直向上 | |
| B. | 小球从A点运动到B点的过程中电场力一直做负功 | |
| C. | 小球从A点运动到B点的过程中通过O点时速度最大 | |
| D. | 小球通过B点时的速度为$\sqrt{{{v}_{0}}^{2}+4gh}$ |
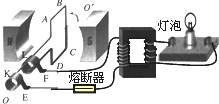 如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )| A. | 中性面位置穿过线框的磁通量为零 | |
| B. | 线框中产生交变电压的有效值为500$\sqrt{2}$V | |
| C. | 变压器原、副线圈匝数之比为25:22 | |
| D. | 允许变压器输出的最大功率为5000W |
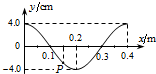 图示为xoy平面内沿x轴传播的简谐横波在t0=0时刻的波形图象,其波速v=5.0m/s.此时平衡位置xp=0.15m的P点正在向-y方向运动,则该波的传播方向是-x(选填“+x”或“-x”),经过△t=0.05s时间P点的加速度第一次达到最大且指向y轴负方向.
图示为xoy平面内沿x轴传播的简谐横波在t0=0时刻的波形图象,其波速v=5.0m/s.此时平衡位置xp=0.15m的P点正在向-y方向运动,则该波的传播方向是-x(选填“+x”或“-x”),经过△t=0.05s时间P点的加速度第一次达到最大且指向y轴负方向. 用如图所示装置可验证机械能守恒定律.轻绳两端系着质量相等的物块A、B,物块B上放置一金属片C.铁架台上固定一金属圆环,圆环处在物块B正下方.系统静止时,金属片C与圆环间的高度差为h.由此释放B,系统开始运动,当物块B穿过圆环时,金属片C被搁置在圆环上.两光电门固定在铁架台上的P1、P2处,通过数字计时器可测出物块B通过P1、P2这段距离的时间.
用如图所示装置可验证机械能守恒定律.轻绳两端系着质量相等的物块A、B,物块B上放置一金属片C.铁架台上固定一金属圆环,圆环处在物块B正下方.系统静止时,金属片C与圆环间的高度差为h.由此释放B,系统开始运动,当物块B穿过圆环时,金属片C被搁置在圆环上.两光电门固定在铁架台上的P1、P2处,通过数字计时器可测出物块B通过P1、P2这段距离的时间.