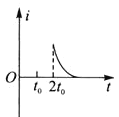
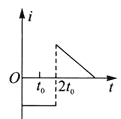
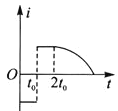
��Ŀ����
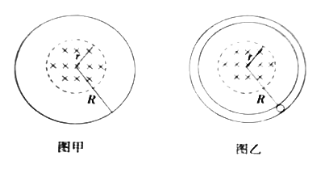
����Ŀ����ͼ��ʾ��������Ȧ����N��100 �ѣ�ab��30 cm��ad��20 cm����ǿ�ų��ĴŸ�Ӧǿ��B��0.8 T���ƴ�ֱ�ų��������OO����ͼʾλ�ÿ�ʼ����ת�������ٶ�����100�� rad/s������
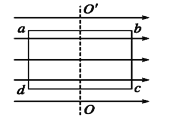
(1)������Ȧ�Ĵ�ͨ�����ֵ��mΪ�����Ȧת��ʲôλ��ʱȡ�ô�ֵ��
(2)��Ȧ�����ĸ�Ӧ�綯�����ֵEmΪ�����Ȧת��ʲôλ��ʱȡ�ô�ֵ��
(3)д����Ӧ�綯��e��ʱ��仯�ı���ʽ��
���𰸡�(1) ![]() Wb ����Ȧλ��������ʱ����ͨ����� (2)
Wb ����Ȧλ��������ʱ����ͨ����� (2) ![]() V ����Ȧλ��ͼʾλ��ʱ������Ȧƽ����ų�����ƽ��ʱ����Ӧ�綯����� (3)
V ����Ȧλ��ͼʾλ��ʱ������Ȧƽ����ų�����ƽ��ʱ����Ӧ�綯����� (3) ![]() V
V
��������
(1)����Ȧλ��������ʱ����ͨ�����![]() ���������ݵã�
���������ݵã�![]() Wb
Wb
(2)����Ȧλ��ͼʾλ��ʱ������Ȧƽ����ų�����ƽ��ʱ����Ӧ�綯�����![]()
![]() ���������ݵã�
���������ݵã�![]()
(3)��ͼʾλ�ÿ�ʼ���綯�ư����ҹ��ɱ仯������![]() ���������ݵã�
���������ݵã�![]()

����Ŀ��ijͬѧ�����о��ȱ���ֱ���˶�����ʵ���У��ô���ʱ����¼�˱�С���϶���ֽ�����˶��������ֽ����ȷ����A��B��C��D��E��F��G��7�������㣬�����������ľ�����ͼ����ʾ��ÿ�������ڵļ�����֮���ʱ������Ϊ0.10s��
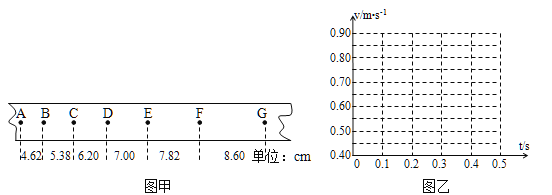
��1���Ը���ֽ���ϸ����������ľ��룬�������B��C��D��E��F�����ʱС����˲ʱ�ٶȣ��뽫D����ٶ�ֵ��������ı����ڣ�������С�������λ����
��������� | B | C | D | E | F |
�������Ӧ��ʱ��t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
ͨ��������ʱС�����ٶ�v/ms��1 | 0.50 | 0.58 | 0.74 | 0.82 |
��2����A��Ϊ��ʱ��㣬��B��C��D��E��F����ʱ�̵�˲ʱ�ٶȱ�����ͼ����ʾ������ֽ�ϣ�������С����˲ʱ�ٶ�v��ʱ��t�仯�Ĺ�ϵͼ�ߣ�
��3�����ݵڣ�2�����л�����v��tͼ�ߣ����С���˶��ļ��ٶȴ�Сa= m/s2��������λ��Ч���֣���