题目内容
【题目】为了探究加速度与力、质量的关系：
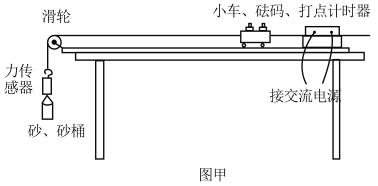
（1）小亮利用如图甲所示的实验方案，探究小车质量一定时加速度与合外力之间的关系，图中上下两层水平轨道，细线跨过滑轮并挂上砝码盘，将砝码和砝码盘的总重作为小车所受合外力，两小车尾部细线连到控制装置上，实验时通过控制装置使两小车同时开始运动，并同时停止。
①实验前，下列操作必要的是
A．选用质量不同的两辆小车
B．调节定滑轮的高度，使细线与轨道平行
C．使砝码和砝码盘的总质量远小于小车的质量
D．将轨道右端适当垫高，使小车在没有细线牵引时能在轨道上匀速运动，以平衡摩擦力
②他测量了两小车的位移为x1，x2，则
= 。
（2）小明用如图乙所示的装置进行实验
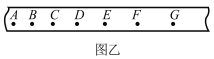
①打出的一条纸带如图丙所示，计时器打点的时间间隔为0.02 s。他从比较清晰的A点起，每五个点取一个计数点，测量出各点到A点的距离标在纸带上各点的下方，则小车运动的加速度为__________m/s2。（计算结果保留两位有效数字）
②实验前由于疏忽，小明遗漏了平衡摩擦力这一步骤，他测量得到的a–F图象，可能是丁图中的图线 （选填“1”、“2”、“3”）。
③调整正确后，他作出的a–F图象末端明显偏离直线，如果已知小车质量为M，某次所挂钩码质量为m，则戊图中坐标a1应为 ，a2应为 。
【答案】（1）①BCD ②
（2）①0.40 ②3 ③
【解析】（1）本实验需要用砝码盘和砝码的重力代替小车所受的合外力，当小车在轨道上滑动时将会与垫高，使小车在没有细线牵引时能在轨道上匀速运动，且应该满足砝码盘和砝码的总质量远小于小车的质量，细线的拉力为小车的合力，要求细线与木板平行，所以应调节定滑轮的高度使细线与木板平行，对小车质量是否相同没有要求，故A错误，BCD正确。小车做初速度为零的匀加速直线运动：由位移与时间关系：x=
at2，因运动时间相等，则位移与加速度成正比。小车1、2的加速度之比为：。
（2）①每五个点取一个计数点，所以相邻的计数点间的时间间隔T=0.1 s，根据匀变速直线运动的推论公式Δx=aT2得
。
②遗漏了平衡摩擦力这一步骤，就会出现当有拉力时，物体不动的情况，由牛顿第二定律可知，即F≠0时，a=0。故图线为：3。
③没有偏离直线时，可以用砝码盘和砝码的总重力代替小车受到的合力，根据牛顿第二定律得：mg=Ma1， 解得。偏离直线后说明砝码的总质量不是远远小于车的质量了，把砝码以及小车看成一个整体，根据牛顿第二定律:mg=（m+M）a2，解得。
